题目内容
12.双曲线2x2-y2=8的实半轴长与虚轴长之比为$\frac{\sqrt{2}}{4}$.分析 根据题意,将双曲线的方程变形为标准方程,可得a=$\sqrt{4}$=2,b=$\sqrt{8}$=2$\sqrt{2}$,进而可得该双曲线的实半轴长与虚轴长,将其相比即可得答案.
解答 解:根据题意,双曲线的方程为2x2-y2=8,变形可得$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{8}$=1,
则有a=$\sqrt{4}$=2,b=$\sqrt{8}$=2$\sqrt{2}$,
即该双曲线的实半轴长为2,虚轴长为2b=4$\sqrt{2}$,
则其实半轴长与虚轴长之比$\frac{a}{2b}$=$\frac{2}{4\sqrt{2}}$=$\frac{\sqrt{2}}{4}$;
故答案为:$\frac{{\sqrt{2}}}{4}$.
点评 本题考查双曲线的几何性质,关键是利用双曲线的方程求出双曲线的实半轴长与虚轴长.

练习册系列答案
相关题目
2.若变量x,y满足约束条件$\left\{\begin{array}{l}y≥x\\ x+y≤2\\ x≥a.\end{array}\right.$且目标函数z=2x-y的最大值是最小值的2倍,则a的值是( )
| A. | $\frac{1}{2}$ | B. | 4 | C. | 3 | D. | $\frac{4}{5}$ |
3. 如图,在△ABC中,AB=AC=2,BC=$\sqrt{2}$,且A在平面α上,B、C在平面α的同侧,M为BC的中点,若△ABC在平面α上的射影是以A为直角顶点的△AB′C′,则AM与平面α所成角的正弦值的取值范围是( )
如图,在△ABC中,AB=AC=2,BC=$\sqrt{2}$,且A在平面α上,B、C在平面α的同侧,M为BC的中点,若△ABC在平面α上的射影是以A为直角顶点的△AB′C′,则AM与平面α所成角的正弦值的取值范围是( )
 如图,在△ABC中,AB=AC=2,BC=$\sqrt{2}$,且A在平面α上,B、C在平面α的同侧,M为BC的中点,若△ABC在平面α上的射影是以A为直角顶点的△AB′C′,则AM与平面α所成角的正弦值的取值范围是( )
如图,在△ABC中,AB=AC=2,BC=$\sqrt{2}$,且A在平面α上,B、C在平面α的同侧,M为BC的中点,若△ABC在平面α上的射影是以A为直角顶点的△AB′C′,则AM与平面α所成角的正弦值的取值范围是( )| A. | [$\frac{\sqrt{42}}{7}$,1) | B. | [$\frac{\sqrt{42}}{7}$,1] | C. | [$\frac{\sqrt{42}}{7}$,$\frac{\sqrt{14}}{4}$] | D. | [$\frac{\sqrt{42}}{7}$,$\frac{\sqrt{14}}{4}$) |
7.命题“?x0∈(0,+∞),lnx0=x0-1”的否定是( )
| A. | ?x∈(0,+∞),lnx≠x-1 | B. | ?x∉(0,+∞),lnx=x-1 | ||
| C. | ?x0∈(0,+∞),lnx0≠x0-1 | D. | ?x0∉(0,+∞),lnx0=x0-1 |
4.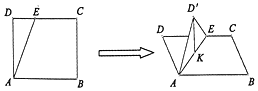 如图,在正方形ABCD中,AB=2,E为线段CD上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则点K所形成轨迹的长度为( )
如图,在正方形ABCD中,AB=2,E为线段CD上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则点K所形成轨迹的长度为( )
 如图,在正方形ABCD中,AB=2,E为线段CD上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则点K所形成轨迹的长度为( )
如图,在正方形ABCD中,AB=2,E为线段CD上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则点K所形成轨迹的长度为( )| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
1.设f(x)是定义在R上的偶函数,对x∈R,都有f(x-2)=f(x+2),且当x∈[-2,0]时,f(x)=($\frac{1}{2}$)x-1,若在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0(a>1)恰有3个不同的实数根,则a的取值范围是( )
| A. | (2,3) | B. | $(\root{3}{3},2)$ | C. | $(\root{3}{4},2)$ | D. | $(\root{3}{2},3)$ |
2.函数f(x)=xlnx的单调递减区间为( )
| A. | $(0,\frac{1}{e})$ | B. | $(-∞,\frac{1}{e})$ | C. | (-∞,-e) | D. | $(\frac{1}{e},+∞)$ |
 如图,四棱锥P-ABCD的底面ABCD为正方形,PA⊥底面ABCD,E,F分别是AC,PB的中点,PA=AB=2.
如图,四棱锥P-ABCD的底面ABCD为正方形,PA⊥底面ABCD,E,F分别是AC,PB的中点,PA=AB=2.