题目内容
设函数 .
.
(1)若x= 时,
时, 取得极值,求
取得极值,求 的值;
的值;
(2)若 在其定义域内为增函数,求
在其定义域内为增函数,求 的取值范围;
的取值范围;
(3)设 ,当
,当 =-1时,证明
=-1时,证明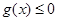 在其定义域内恒成立,并证明
在其定义域内恒成立,并证明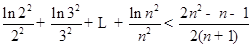 (
( ).
).
(1) .(2)
.(2) .
.
(3)转化成 .所以
.所以 .通过“放缩”,“裂项求和”。
.通过“放缩”,“裂项求和”。
解析试题分析: ,
,
(1)因为 时,
时, 取得极值,所以
取得极值,所以 ,
,
即 故
故 . 3分
. 3分
(2) 的定义域为
的定义域为 ,
,
要使 在定义域
在定义域 内为增函数,
内为增函数,
只需在 内有
内有 恒成立,
恒成立,
即 在
在 恒成立, 5分
恒成立, 5分
又 7分
7分 ,
,
因此,若 在其定义域内为增函数,则
在其定义域内为增函数,则 的取值范围是
的取值范围是 . 9分
. 9分
(3)证明: ,
,
当 =-1时,
=-1时, ,其定义域是
,其定义域是 ,
,
令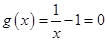 ,得
,得 .
.
则 在
在 处取得极大值,也是最大值.
处取得极大值,也是最大值.
而 .所以
.所以 在
在 上恒成立.因此
上恒成立.因此 .
.
因为 ,所以
,所以 .
.
则 .
.
所以
= <
<
= =
= .
.
所以结论成立. 13分
考点:利用导数研究函数的单调性、极值,不等式恒成立问题,不等式的证明。。
点评:难题,利用导数研究函数的单调性、极值,是导数应用的基本问题,主要依据“在给定区间,导函数值非负,函数为增函数;导函数值非正,函数为减函数”。确定函数的极值,遵循“求导数,求驻点,研究单调性,求极值”。不等式恒成立问题,往往通过构造函数,研究函数的最值,使问题得到解决。本题不等式证明过程中,利用“放缩法”,转化成易于求和的数列,体现解题的灵活性。

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
 为偶函数.
为偶函数.  的值;
的值; 有且只有一个根, 求实数
有且只有一个根, 求实数 的取值范围.
的取值范围.  的图象与x轴,y轴无交点且关于原点对称,又有函数f(x)=x2-alnx+m-2在(1,2]上是增函数,g(x)=x-
的图象与x轴,y轴无交点且关于原点对称,又有函数f(x)=x2-alnx+m-2在(1,2]上是增函数,g(x)=x- 在(0,1)上为减函数.
在(0,1)上为减函数. ,数列{an}满足a1=1,an+1=p(an),(n∈N+),数列{bn},满足
,数列{an}满足a1=1,an+1=p(an),(n∈N+),数列{bn},满足 ,
, ,求数列{an}的通项公式an和sn.
,求数列{an}的通项公式an和sn. ,试比较[h(x)]n+2与h(xn)+2n的大小(n∈N+),并说明理由.
,试比较[h(x)]n+2与h(xn)+2n的大小(n∈N+),并说明理由.

 .
. 的单调区间;
的单调区间; ,对
,对 都有
都有 成立,求实数
成立,求实数 的取值范围;
的取值范围; (
( 且
且 ).
).
 若函数
若函数 在
在 和
和 上是增函数,在
上是增函数,在 是减函数,求
是减函数,求 的值;
的值; 讨论函数
讨论函数 的单调递减区间;
的单调递减区间; 如果存在
如果存在 ,使函数
,使函数 ,
,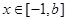
 ,在
,在 处取得最小值,试求
处取得最小值,试求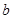 的最大值.
的最大值. .
. 在每段区间上的解析式,并在图中的直角坐标系中作出函数
在每段区间上的解析式,并在图中的直角坐标系中作出函数 对任意的实数
对任意的实数 恒成立,求实数
恒成立,求实数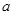 的取值范围.
的取值范围.
 满足:
满足: (
( ),
), ,求
,求 的值,并用数学归纳法证明:对任意的
的值,并用数学归纳法证明:对任意的 ,均有:
,均有: .
. ,
, 的解集
的解集 .求
.求 的值;
的值; 求
求 的最小值.
的最小值. ,
, ,函数
,函数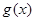 的图像在点
的图像在点 处的切线平行于
处的切线平行于 轴.
轴. 的值;
的值; 的直线与函数
的直线与函数 的图象交于两点
的图象交于两点 ,(
,( )
) .
.