题目内容
已知函数
 若函数
若函数 在
在 和
和 上是增函数,在
上是增函数,在 是减函数,求
是减函数,求 的值;
的值; 讨论函数
讨论函数 的单调递减区间;
的单调递减区间; 如果存在
如果存在 ,使函数
,使函数 ,
,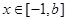
 ,在
,在 处取得最小值,试求
处取得最小值,试求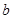 的最大值.
的最大值.

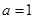 ;
; 当
当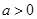 时,单调减区间为
时,单调减区间为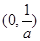 当
当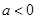 时,单调减区间为
时,单调减区间为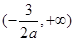 ;
;
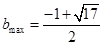 .
.
解析试题分析: 通过求导以及极值点的导数计算
通过求导以及极值点的导数计算 的值为1;
的值为1; 通过导数与函数的单调性关系讨论函数
通过导数与函数的单调性关系讨论函数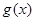 的单调减区间;
的单调减区间; 先写出
先写出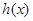 函数表达式,是一个三次多项式.由
函数表达式,是一个三次多项式.由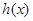 ,
,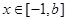 在
在 处取得最小值知
处取得最小值知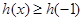 在区间
在区间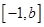 上恒成立,从而得
上恒成立,从而得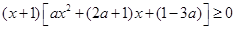 再讨论
再讨论 与
与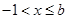 时利用二次函数在闭区间的最值问题解得
时利用二次函数在闭区间的最值问题解得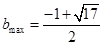 .
.
试题解析:(Ⅰ)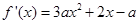 1分
1分 函数
函数 在
在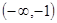 和
和 上是增函数,在
上是增函数,在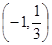 上是减函数,
上是减函数,
∴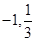 为
为 的两个极值点,∴
的两个极值点,∴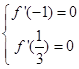 即
即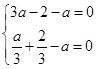 3分
3分
解得: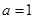 4分
4分
(Ⅱ)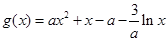 ,
,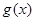 的定义域为
的定义域为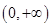 ,
,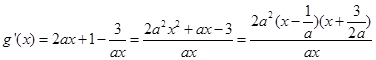 5分
5分
当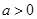 时,由
时,由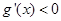 解得
解得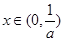 ,
,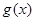 的单调减区间为
的单调减区间为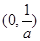 7分
7分
当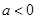 时,由
时,由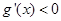 解得
解得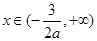 ,
,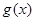 的单调减区间为
的单调减区间为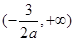 9分
9分
(Ⅲ) ,据题意知
,据题意知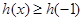 在区间
在区间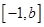 上恒成立,即
上恒成立,即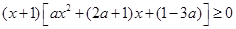 ① 10分
① 10分
当 时,不等式①成立;
时,不等式①成立;
当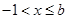 时,不等式①可化为
时,不等式①可化为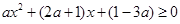 ② 11分
② 11分
令 ,由于二次函数
,由于二次函数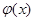 的图象是开口向下的抛物线,故它在闭区间上的最小值必在端点处取得,又
的图象是开口向下的抛物线,故它在闭区间上的最小值必在端点处取得,又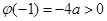 ,所以不等式②恒成立的充要条件是
,所以不等式②恒成立的充要条件是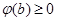 ,即
,即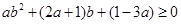 12分
12分
即 ,因为这个关于
,因为这个关于 的不等式在区间
的不等式在区间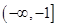 上有解,所以
上有解,所以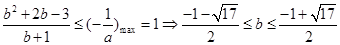 13分
13分
又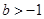 ,故
,故
练习册系列答案
相关题目
探究函数f(x)=x+ ,x∈(0,+∞)的最小值,并确定取得最小值时x的值.列表如下:
,x∈(0,+∞)的最小值,并确定取得最小值时x的值.列表如下:
| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.02 | 4.04 | 4.3 | 5 | 5.8 | 7.57 | … |
函数f(x)=x+
 (x>0)在区间(0,2)上递减;
(x>0)在区间(0,2)上递减;(1)函数f(x)=x+
 (x>0)在区间 上递增.
(x>0)在区间 上递增.当x= 时,y最小= .
(2)证明:函数f(x)=x+
 在区间(0,2)上递减.
在区间(0,2)上递减.(3)思考:函数f(x)=x+
 (x<0)有最值吗?如果有,那么它是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
(x<0)有最值吗?如果有,那么它是最大值还是最小值?此时x为何值?(直接回答结果,不需证明) 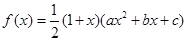 ,
,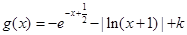
 的图像关于
的图像关于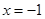 对称,且
对称,且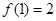 ,求
,求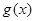 的图像的交点个数.
的图像的交点个数. (
( )在区间
)在区间 上有最大值
上有最大值 和最小值
和最小值 .设
.设 .
. 、
、 的值;
的值; 在
在 上有解,求实数
上有解,求实数 的取值范围.
的取值范围. ,若在定义域内存在实数
,若在定义域内存在实数 ,满足
,满足 ,则称
,则称 ,试判断
,试判断 是定义在区间
是定义在区间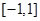 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数 的取值范围;
的取值范围; 为定义域
为定义域 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数
 时,讨论函数
时,讨论函数 的单调性:
的单调性: 的图像上存在不同两点
的图像上存在不同两点 ,设线段
,设线段 的中点为
的中点为 ,使得
,使得 处的切线
处的切线 与直线
与直线 .
. 时,
时, 取得极值,求
取得极值,求 的值;
的值; ,当
,当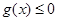 在其定义域内恒成立,并证明
在其定义域内恒成立,并证明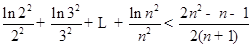 (
( ).
). ,
, )时,f(x)≤g(x),求a的取值范围.
)时,f(x)≤g(x),求a的取值范围.  ,
,
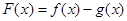 的单调区间;
的单调区间; 时,函数
时,函数 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; 满足
满足 .求证:
.求证: .
.