题目内容
1.定义区间I=(α,β)的长度为β-α,已知函数f(x)=ax2+(a2+1)x,其中a<0,区间I={x|f(x)>0}.(Ⅰ)求区间I的长度;
(Ⅱ)设区间I的长度函数为g(a),试判断函数g(a)在(-∞,-1]上的单调性;
(Ⅲ)在上述函数g(a)中,若a∈(-∞,-1],问:是否存在实数k,使得g(k-sinx-3)≤g(k2-sin2x-4)对一切x∈R恒成立,若存在,求出k的范围;若不存在,请说明理由.
分析 (Ⅰ)解不等式f(x)>0,可得区间I的长度;
(Ⅱ)由(I)知$g(a)=-a-\frac{1}{a}$,a∈(-∞,-1],根据定义法,可证得函数g(a)在(-∞,-1]上为减函数;
(Ⅲ)设存在实数k,使得g(k-sinx-3)≤g(k2-sin2x-4)对一切x∈R恒成立,则$\left\{{\begin{array}{l}{k-sinx-3≤-1}\\{{k^2}-{{sin}^2}x-4≤-1}\\{k-sinx-3≤{k^2}-{{sin}^2}x-4}\end{array}}\right.$,解得答案.
解答 (本小题满分13分)
解:(Ⅰ)f(x)>0,即ax2+(a2+1)x>0
∵a<0
∴-ax2-(a2+1)x<0
⇒-x[ax+(a2+1)]<0…(2分)
∴$0<x<-\frac{{{a^2}+1}}{a}$,即$I=({0,-\frac{{{a^2}+1}}{a}})$…(3分)
∴I的长度为$-\frac{{{a^2}+1}}{a}=-a-\frac{1}{a}$…(4分)
(Ⅱ)由(I)知$g(a)=-a-\frac{1}{a}$,a∈(-∞,-1]
设任意的a1,a2∈(-∞,-1]且a1<a2,则…(5分)
g(a1)-g(a2)=$({-{a_1}-\frac{1}{a_1}})-({-{a_2}-\frac{1}{a_2}})$=$({{a_2}-{a_1}})•\frac{{{a_1}{a_2}-1}}{{{a_1}{a_2}}}$…(6分)
∵a1<a2≤-1,
∴a1a2>1,
∴a1a2-1>0,又a2-a1>0…(7分)
∴$({{a_2}-{a_1}})•\frac{{{a_1}{a_2}-1}}{{{a_1}{a_2}}}>0$,即g(a1)>g(a2)
∴函数g(a)在(-∞,-1]上为减函数.…(8分)
(说明:如果运用对勾函数的知识解决问题,参照给分)
(Ⅲ)设存在实数k,使得g(k-sinx-3)≤g(k2-sin2x-4)对一切x∈R恒成立,
则$\left\{{\begin{array}{l}{k-sinx-3≤-1}\\{{k^2}-{{sin}^2}x-4≤-1}\\{k-sinx-3≤{k^2}-{{sin}^2}x-4}\end{array}}\right.$
⇒$\left\{{\begin{array}{l}{k≤sinx+2}\\{{k^2}≤{{sin}^2}x+3}\\{{k^2}-k-1≤{{sin}^2}x-sinx}\end{array}}\right.$…(10分)
$⇒\left\{{\begin{array}{l}{k≤1}\\{-\sqrt{3}≤k≤\sqrt{3}}\\{-\frac{1}{2}≤k≤\frac{3}{2}}\end{array}}\right.$$⇒-\frac{1}{2}≤k≤1$…(12分)
∴存在实数$k∈[{-\frac{1}{2},1}]$使得g(k-sinx-3)≤g(k2-sin2x-4)对一切x∈R恒成立…(13分)
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.

| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
| A. | (-1,2) | B. | [-1,+∞) | C. | (-∞,2] | D. | [-1,2] |
| A. | 7π | B. | 14π | C. | 28π | D. | 36π |
| A. | 46 | B. | 56 | C. | 66 | D. | 76 |
| A. | 若K2的观测值为k=6.635,我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病 | |
| B. | 若从统计量中求出有95%的把握认为吸烟与患肺病有关系,是指有5%的可能性使得推断出现错误 | |
| C. | 从独立性检验可知有99%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有99%的可能患有肺病 | |
| D. | 以上三种说法都不正确 |
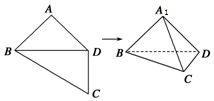 如图,四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A1-BCD,则四面体A1-BCD的体积的最大值为$\frac{1}{6}$,此时A1C与平面A1BD所成的角为45°.
如图,四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A1-BCD,则四面体A1-BCD的体积的最大值为$\frac{1}{6}$,此时A1C与平面A1BD所成的角为45°.