题目内容
12.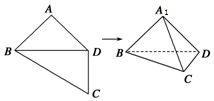 如图,四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A1-BCD,则四面体A1-BCD的体积的最大值为$\frac{1}{6}$,此时A1C与平面A1BD所成的角为45°.
如图,四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A1-BCD,则四面体A1-BCD的体积的最大值为$\frac{1}{6}$,此时A1C与平面A1BD所成的角为45°.
分析 先根据条件证明△A1CD为等腰直角三角形,得到∠A1DC=45°,即可得到A1C与平面A1CD所成的角为45°,
再求出△A1BD的面积,根据体积公式即可出四面体A1-BCD的体积
解答 解:∵四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,
由BD⊥CD,平面A1BD⊥平面BCD,易得CD⊥平面A1BD,
∴CD⊥A1B,CD⊥A1D,
∵A1D=CD,
∴△A1CD为等腰直角三角形,
∴∠A1DC=45°,
则A1C与平面A1BD所成的角为45°,
又由AB=AD,BD=$\sqrt{2}$,
∵四面体A1-BCD的体积V=$\frac{1}{3}$CD•S△A1BD=$\frac{1}{3}$=$\frac{1}{6}$
故答案为:$\frac{1}{6}$,45°
点评 本题考查了棱锥的结构特征,以及棱柱的结构特征,熟练掌握空间位置关系与距离的判定是解本题的关键.

练习册系列答案
相关题目
2.已知函数f(x)=ax3+bx2+cx+d的图象与x轴有三个不同交点(0,0),(x1,0),(x2,0),且f(x)在x=1,x=2时取得极值,则x1•x2的值为( )
| A. | 4 | B. | 5 | C. | 6 | D. | 不确定 |
4.已知O为△ABC的外心,AB=3,AC=4,$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,且2x+y=1(x,y≠0),则cos∠BAC=( )
| A. | $\frac{3}{8}$ | B. | $\frac{3}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |
2.函数f(x)=x2-2lnx的单调递减区间为( )
| A. | (0,1) | B. | (-1,1) | C. | (0,+∞) | D. | (1,+∞) |
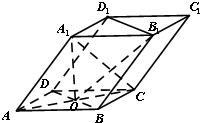 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1=$\sqrt{2}$.
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1=$\sqrt{2}$.