题目内容
已知集合A={x||x|≤a，a＞0}，集合B={-2，-1，0，1，2}，且A∩B={-1，0，1}，则a的取值范围是（ ）
| A、（1，2） |
| B、[1，2） |
| C、（1，2] |
| D、（0，1] |
考点：交集及其运算
专题：集合
分析：首先化简集合A，然后根据交集的定义即可求解．
解答：
解：∵B={-2，-1，0，1，2}，A∩B={-1，0，1}，
集合A={x||x|≤a，a＞0}={x|-a≤x≤a}
∴2＜a≤1
故选：B．
集合A={x||x|≤a，a＞0}={x|-a≤x≤a}
∴2＜a≤1
故选：B．
点评：本题主要考查集合关系中参数的取值范围问题，两个集合的交集的定义，属于基础题．
练习册系列答案
相关题目
y=xsinx+cosx在下面哪个区间内是减函数（ ）
A、（
| ||||
| B、（0，π） | ||||
C、（
| ||||
D、（-
|
圆x2+y2+4x+26y+b2=0与某坐标轴相切，那么b可以取得值是（ ）
| A、±2或±13 | B、1和2 |
| C、-1和-2 | D、-1和1 |
某几何体的三视图如图所示，则该几何体的体积是（ ）
| A、π | B、2π | C、4π | D、8π |
函数f（x）=2x-1+
的值域为（ ）
| x+1 |
| A、[-4，+∞） | ||
B、[-
| ||
| C、[-1，+∞） | ||
| D、[-3，+∞） |
如图，已知四边形ABCD的直观图是一个边长为1的正方形，则原图形的周长为（ ）
A、2
| ||
| B、6 | ||
| C、8 | ||
D、4
|
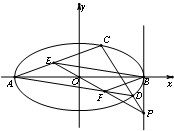如图，在平面直角坐标系xOy中，A、B分别是椭圆：