题目内容
已知点O（0，0），A（-2，a）（a∈R是常数），动点P满足
•
=3．
（1）求动点P的轨迹；
（2）若直线l：x+2y-2=0上有且仅有一点Q，使
•
=3，求常数a的值；并求此时直线l与直线OA夹角的余弦值．
| PO |
| PA |
（1）求动点P的轨迹；
（2）若直线l：x+2y-2=0上有且仅有一点Q，使
| QO |
| QA |
考点：平面向量数量积的运算
专题：平面向量及应用,圆锥曲线的定义、性质与方程
分析：（1）设P（x，y），则
=(-x，-y)，
=(-2-x，a-y)，再利用数量积运算即可得出；
（2）设P（x，y），由
•
=3，可得-x（-2-x）+（-y）（a-y）=3．与直线l的方程联立，利用△=0即可解出．再利用向量夹角公式即可得出．
| PO |
| PA |
（2）设P（x，y），由
| QO |
| QA |
解答：
解：（1）设P（x，y），则
=(-x，-y)，
=(-2-x，a-y)，
由
•
=3得-x（-2-x）+（-y）（a-y）=3，
即(x+1)2+(y-
)2=4+
a2，
∵4+
a2＞0，∴点P的轨迹为圆．
（2）设P（x，y），由
•
=3，可得-x（-2-x）+（-y）（a-y）=3．
与直线l的方程联立可得：
化为（2y-2）（2y-4）+y2-ay-3=0，
化为5y2-（a+12）y+5=0，
依题意，△=[-（a+12）]2-4×5×5=0，
解得a=-2或a=-22．
直线l与坐标轴的交点分别为M（2，0），N（0，1），
=(-2，1)．）
直线l与直线OA夹角的余弦值cosθ=
=
，
a=-2时，cosθ=
；
a=-22时，cosθ=
．
| PO |
| PA |
由
| PO |
| PA |
即(x+1)2+(y-
| a |
| 2 |
| 1 |
| 4 |
∵4+
| 1 |
| 4 |
（2）设P（x，y），由
| QO |
| QA |
与直线l的方程联立可得：
|
化为（2y-2）（2y-4）+y2-ay-3=0，
化为5y2-（a+12）y+5=0，
依题意，△=[-（a+12）]2-4×5×5=0，
解得a=-2或a=-22．
直线l与坐标轴的交点分别为M（2，0），N（0，1），
| MN |
直线l与直线OA夹角的余弦值cosθ=
|
| ||||
|
|
| |a+4| | ||||
|
a=-2时，cosθ=
| ||
| 10 |
a=-22时，cosθ=
9
| ||
| 610 |
点评：本题考查了数量积运算、直线与抛物线相切转化为方程联立得到△=0、向量夹角公式等基础知识与基本技能方法，考查了推理能力和计算能力，属于难题．
练习册系列答案
阅读快车系列答案
相关题目
已知命题p：?x0＞0，lnx0＜0．则￢p为（ ）
| A、?x＞0，lnx≥0 |
| B、?x≤0，lnx≥0 |
| C、?x0＞0，lnx0≥0 |
| D、?x0≤0，lnx0＜0 |
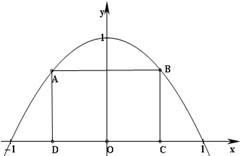如图所示，抛物线y=1-x2与x轴所围成的区域是一块等待开垦的土地，现计划在该区域内围出一块矩形地块ABCD作为工业用地，其中A、B在抛物线上，C、D在x轴上．已知工业用地每单位面积价值为3a元（a＞0），其它的三个边角地块每单位面积价值a元．
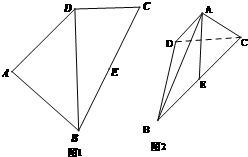如图，四边形ABCD中（图1），E是BC的中点，DB=2，DC=1，BC=