题目内容
设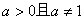
，则“函数
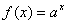在R上是减函数 ”，是“函数
在R上是增函数”的（ ）
A. 充分不必要条件 B. 必要不充分条件 C. 充分必要条件 D. 既不充分也不必要条件
A
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
全优考典单元检测卷及归类总复习系列答案题目内容
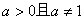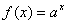设，则“函数在R上是减函数 ”，是“函数在R上是增函数”的（ ）
A. 充分不必要条件 B. 必要不充分条件 C. 充分必要条件 D. 既不充分也不必要条件
A
全优考典单元检测卷及归类总复习系列答案
满足
且
的通项公式；
，
，则
+1的取值范围是( )
） B. （
，
，
，+
）
：
（
）的焦距为
，且过点（
，
），右焦点为
．设
，
是
的中点
的横坐标为
，
线段
，
两点．
（Ⅰ）求椭圆
的取值范围．
表示两个不同的平面，
表示两条不同的直线，则
的一个充分条件是（ ）
B.
C.
D.
，对函数
，定义
关于
的“对称函数”为函数
，
满足：对任意
，两个点
关于点
对称，若
是
关于
的“对称函数”，且
恒成立，则实数
的取值范围是
. 
＝（
），
＝（cosA,sinA）.若
，且acosB + bcosA =csinC，则角
＝ . 
.
，且sin α＝
，求f(α)的值；