题目内容
11．正方体ABCD-A1B1C1D1中，A1C与截面DBC1交于O点，AC，BD交于M点．（1）求证：A、M、A1、C1四点共面；
（2）求证：C1、O、M三点共线．
分析 （1）由A1C1∥AM，能证明A、M、A1、C1四点共面
（2）推导出C1、M、O都是平面A1ACC1和平面DBC1的公共点，由此能证明C1，O，M三点共线．
解答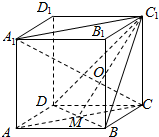 
证明：（1）∵正方体ABCD-A1B1C1D1中，
A1C与截面DBC1交于O点，AC，BD交于M点，
∴A1C1∥AM，
∴A、M、A1、C1四点共面
（2）证明：∵C1∈平面A1ACC1，且C1∈平面DBC1，
∴C1是平面A1ACC1与平面DBC1的公共点．
又∵M∈AC，∴M∈平面A1ACC1．
∵M∈BD，∴M∈平面DBC1，
∴M也是平面A1ACC1与平面DBC1的公共点，
∴C1M是平面A1ACC1与平面DBC1的交线．
∵O为 A1C与截面DBC1的交点，
∴O∈平面A1ACC1，O∈平面DBC1，
即O也是两平面的公共点，
∴O∈直线C1M，即C1，O，M三点共线．
点评 本题考查四点共面的证明，考查三点共线的证明，是基础题，解题时要认真审题，注意平面的基本性质及推论的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
2．已知A（1，1，2），B（-1，2，1），O为坐标原点，则向量$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角是（ ）
| A． | 0 | B． | $\frac{π}{3}$ | C． | π | D． | $\frac{π}{2}$ |
在四棱锥P-ABCD中，已知PA⊥平面ABCD，PB与平面ABC成60°的角，底面ABCD是直角梯形，∠ABC=∠BAD=90°，AB=BC=$\frac{1}{2}$AD．