题目内容

已知sinα=
1
3
，则cos2（
α
2
+
π
4
）=（　　）
A、
1
6
B、
2
3
C、
1
3
D、
1
2
考点：二倍角的余弦,同角三角函数基本关系的运用
专题：计算题,三角函数的求值
分析：利用cos2（
α
2
+
π
4
）=
1+cos(α+
π
2
)
2
=
1-sinα
2
，代入计算可得结论．
解答： 解：∵sinα=
1
3
，
∴cos2（
α
2
+
π
4
）=
1+cos(α+
π
2
)
2
=
1-sinα
2
=
1
3
，
故选：C．
点评：本题考查二倍角的余弦，考查学生的计算能力，正确运用二倍角的余弦公式是关键．
练习册系列答案
相关题目
已知点P（a+1，b+1），Q（1，0），线段PQ与直线2x-3y+1=0有交点，若存在M∈R+，使得-b-a2≤M恒成立，则M的最小值为
 
．
当n很大时，函数f（x）在区间[
i-1
n
，
i
n
]上的值可以用
 
以直代曲．
设f（x）可导，且y=f（e2x），则y′=（　　）
A、f′（e2x）
B、f′（e2x）e2x
C、2f′（e2x）
D、2f′（e2x）e2x
设y=ln（2x+3），则y′=（　　）
A、
1
2(2x+3)
B、
2
x+3
C、
1
2x+3
D、
2
2x+3
设A是圆形纸片内不同于圆心的一个点，取圆周上一点B，折叠纸片使点B与A重合，得到一条折痕，当点B取遍圆周上所有点时，得到的所有折痕均与某条曲线相切，这条曲线是一个（　　）
A、圆B、椭圆C、双曲线D、抛物线
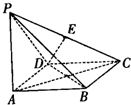四棱锥P-ABCD的底面为棱形，且∠DAB=60°，PA⊥底面ABCD，AB=2a，PA=2
3
a，E为PC的中点．
（1）求直线DE与平面PAC所成角的大小；
（2）求二面角E-AD-C的余弦值．
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的右焦点为F（1，0），短轴的一个端点B到F的距离等于焦距．
（Ⅰ）求椭圆C的方程；
（Ⅱ）过点F的直线l与椭圆C交于不同的两点M，N，是否存在直线l，使得△BFM与△BFN的面积比值为2？若存在，求出直线l的方程；若不存在，说明理由．
已知函数y=f（x）对于任意正实数x，y有f（xy）=f（x）f（y），且x＞1时，f（x）＜1，f（2）=
1
9
（1）求证：f（x）＞0；
（2）求证：y=f（x）在（0，+∞）为单调减函数．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网