题目内容
函数f(x)由x-ln[f(x)+1]=0确定,则导函数y=f′(x)图象的大致形状是( )
A、 |
B、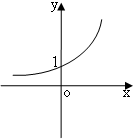 |
C、 |
D、 |
考点:利用导数研究函数的单调性,导数的运算
专题:导数的综合应用
分析:由已知方程结合对数的运算性质求得f(x)的解析式,求导后可得导函数为以e为底数的指数函数,则其图象可求.
解答:
解:由x-ln[f(x)+1]=0,得:ln[f(x)+1]=x,则f(x)=ex-1.
∴f′(x)=ex.
则y=f′(x)图象的大致形状是:

故选:B.
∴f′(x)=ex.
则y=f′(x)图象的大致形状是:

故选:B.
点评:本题考查了导数的运算,考查了指数函数的图象和性质,是基础题.

练习册系列答案
相关题目
方程log
x=2x-2014的实数根的个数为( )
| 1 |
| 2 |
| A、0 | B、1 | C、2 | D、不确定 |
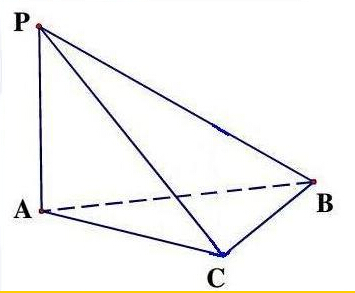 如图所示,在四面体P-ABC中,已知PA=BC=6,PC=AB=10,AC=8,PB=2
如图所示,在四面体P-ABC中,已知PA=BC=6,PC=AB=10,AC=8,PB=2