题目内容
在△ABC中,已知ln(sinA+sinB)=lnsinA+lnsinB-ln(sinB-sinA).且cos(A-B)+cosC=1-cos2C.
(1)试确定△ABC的形状;
(2)求
的取值范围.
(1)试确定△ABC的形状;
(2)求
| a+c |
| b |
考点:三角形的形状判断,正弦定理的应用
专题:解三角形
分析:(1)依题意,利用对数的运算性质可得sin2B-sin2A=sinA•sinB,①,再由两角和与差的余弦及二倍角的余弦公式,由cos(A-B)+cosC=1-cos2C可得sinA•sinB=sin2C,②,联立①②即可判断△ABC的形状;
(2)由(1)知△ABC为Rt△,且B为直角,利用正弦定理及辅助角公式可得
=
sin(A+
),利用正弦函数的单调性即可求得
的取值范围.
(2)由(1)知△ABC为Rt△,且B为直角,利用正弦定理及辅助角公式可得
| a+c |
| b |
| 2 |
| π |
| 4 |
| a+c |
| b |
解答:
解:(1)在△ABC中,∵ln(sinA+sinB)=lnsinA+lnsinB-ln(sinB-sinA),
∴ln[(sinA+sinB)(sinB-sinA)]=ln(sinA•sinB),
∴sin2B-sin2A=sinA•sinB,①
又cos(A-B)+cosC=1-cos2C,
∴cos(A-B)-cos(A+B)=2sinA•sinB=2sin2C,即sinA•sinB=sin2C,②
联立①②得:sin2B-sin2A=sin2C,由正弦定理可得,b2=a2+c2,
∴△ABC为Rt△;
(2)在△ABC中,由(1)知△ABC为Rt△,且B为直角,
由正弦定理得:
=
=sinA+sinC=sinA+sin(
-A)=sinA+cosA=
sin(A+
),
∵A∈(0,
),(A+
)∈(
,
),sin(A+
)∈(
,1],
∴
sin(A+
)∈(1,
],即
的取值范围为:(1,
].
∴ln[(sinA+sinB)(sinB-sinA)]=ln(sinA•sinB),
∴sin2B-sin2A=sinA•sinB,①
又cos(A-B)+cosC=1-cos2C,
∴cos(A-B)-cos(A+B)=2sinA•sinB=2sin2C,即sinA•sinB=sin2C,②
联立①②得:sin2B-sin2A=sin2C,由正弦定理可得,b2=a2+c2,
∴△ABC为Rt△;
(2)在△ABC中,由(1)知△ABC为Rt△,且B为直角,
由正弦定理得:
| a+c |
| b |
| sinA+sinC |
| sinB |
| π |
| 2 |
| 2 |
| π |
| 4 |
∵A∈(0,
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
| ||
| 2 |
∴
| 2 |
| π |
| 4 |
| 2 |
| a+c |
| b |
| 2 |
点评:标题考查三角形的形状判断,考查正弦定理与两角和与差的余弦、二倍角的余弦的综合应用,考查扥就转化思想与运算求解能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
将长、宽分别为4和3的长方形ABCD沿对角线AC折起,得到四面体A-BCD,则四面体A-BCD的外接球的体积为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
用秦九韶算法计算函数f(x)=3x4-2x3-6x-17,当x=2时,则f(x)的值为( )
| A、0 | B、2 | C、3 | D、-3 |
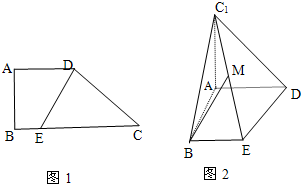 如图1,直角梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=
如图1,直角梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=