题目内容
某港口相邻两次高潮发生的时间间隔12h20min，低潮时入口处水的深度为2.8m，高潮时为8.4m，一次高潮发生在10月 3日2：00．
（1）若从10月3日0：00开始计算时间，选用一个三角函数来近似描述这个港口的水深d（m）和时间t（h）之间的函数关系；
（2）求出10月5日4：00水的深度；
（3）求出10月3日吃水深度为5m的轮船能进入港口的时间．
（1）若从10月3日0：00开始计算时间，选用一个三角函数来近似描述这个港口的水深d（m）和时间t（h）之间的函数关系；
（2）求出10月5日4：00水的深度；
（3）求出10月3日吃水深度为5m的轮船能进入港口的时间．
考点：在实际问题中建立三角函数模型,函数y=Asin（ωx+φ）的图象变换
专题：综合题,三角函数的求值
分析：（1）设d=Asin（ωt+φ）+h，利用低潮时入口处水的深度为2.8m，高潮时为8.4m，求出h，A，利用两次高潮发生的时间间隔12h20min，求出ω，再求出φ，即可描述这个港口的水深d（m）和时间t（h）之间的函数关系；
（2）10月5日4：00，t=24+24+4，即可求出水的深度；
（3）d=2.8sin（
t+
）+5.6≥5，求出10月3日吃水深度为5m的轮船能进入港口的时间．
（2）10月5日4：00，t=24+24+4，即可求出水的深度；
（3）d=2.8sin（
| 6π |
| 37 |
| 13π |
| 74 |
解答：
解：（1）设d=Asin（ωt+φ）+h，则
∴h=5.6，A=2.8，
∵T=12+
=
，
∴ω=
，
t=2时，2ω+φ=
，∴φ=
，
∴d=2.8sin（
t+
）+5.6；
（2）t=24+24+4时，d=2.8sin（
×52+
）+5.6≈8.24；
（3）d=2.8sin（
t+
）+5.6≥5
∴10月3日吃水深度为5m的轮船能进入港口的时间大约为0：00～5：30；10：51～17：48；23：12～24：00．
|
∵T=12+
| 1 |
| 3 |
| 37 |
| 3 |
∴ω=
| 6π |
| 37 |
t=2时，2ω+φ=
| π |
| 2 |
| 13π |
| 74 |
∴d=2.8sin（
| 6π |
| 37 |
| 13π |
| 74 |
（2）t=24+24+4时，d=2.8sin（
| 6π |
| 37 |
| 13π |
| 74 |
（3）d=2.8sin（
| 6π |
| 37 |
| 13π |
| 74 |
∴10月3日吃水深度为5m的轮船能进入港口的时间大约为0：00～5：30；10：51～17：48；23：12～24：00．
点评：本题考查在实际问题中建立三角函数模型，考查学生利用数学知识解决实际问题，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
下列命题错误的是（ ）
| A、命题“若p则q”与命题“若￢q则￢p”互为逆否命题 |
| B、命题“?x∈R，x2-x＞0”的否定是“?x∈R，x2-x≤0” |
| C、命题“若a＜b，则am2＜bm2”的否命题为真 |
| D、命题“若b2=ac，则a，b，c成等比数列”的逆命题为假 |
已知A={x|x=3k-1，k∈Z}，则下面表述正确的是（ ）
| A、5∈A | B、5⊆A |
| C、7∈A | D、7⊆A |
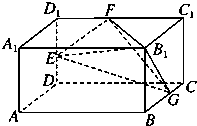如图，长方体AC1中，AB=2，BC=AA1=1．E、F、G分别为棱DD1、D1C1、BC的中点．