题目内容
已知数列{an}是各项均不为0的等差数列,其前n项和为Sn,且an2=S2n-1,数列{bn}满足b1=-
,2bn+1=bn-1.
(Ⅰ)求an,并证明数列{bn+1}是等比数列;
(Ⅱ)若cn=an(bn+1),求数列{cn}的前n项和Tn.
| 1 |
| 2 |
(Ⅰ)求an,并证明数列{bn+1}是等比数列;
(Ⅱ)若cn=an(bn+1),求数列{cn}的前n项和Tn.
考点:数列的求和,等比关系的确定
专题:等差数列与等比数列
分析:(Ⅰ)利用an2=S2n-1,求出数列的前两项,通过等差数列求出通项公式,利用等比数列的定义证明{bn+1}是等比数列.
(Ⅱ)利用等比数列求出通项公式,化简cn=an(bn+1),利用错位相减法求解数列的和即可.
(Ⅱ)利用等比数列求出通项公式,化简cn=an(bn+1),利用错位相减法求解数列的和即可.
解答:
解:(Ⅰ)由an2=S2n-1
令n=1得a12=S1=a1解a1=1
令n=2得a22=S3=3a2,得a2=3
∵{an}为等差数列,∴an=2n-1
证明:∵bn+1≠0,
=
=
=
又b1+1=
,故{bn+1}是以
为首项公比为
的等比数列.
(Ⅱ)由(1)知,∵bn+1=(
)n,
∴cn=(2n-1)(
)n故Tn=(
)1+3×(
)2+5×(
)3+…+(2n-1)(
)n
Tn=(
)2+3×(
)3+…+(2n-3)(
)n+(2n-1)(
)n+1
∴
Tn=(
)1+2[(
)2+(
)3+(
)4+…+(
)n]-(2n-1)(
)n+1
=
-(
)n-1-
(
)n
∴Tn=3-(2n+3)(
)n
令n=1得a12=S1=a1解a1=1
令n=2得a22=S3=3a2,得a2=3
∵{an}为等差数列,∴an=2n-1
证明:∵bn+1≠0,
| bn+1+1 |
| bn+1 |
| ||||
| bn+1 |
| ||
| bn+1 |
| 1 |
| 2 |
又b1+1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)由(1)知,∵bn+1=(
| 1 |
| 2 |
∴cn=(2n-1)(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 3 |
| 2 |
| 1 |
| 2 |
| (2n-1) |
| 2 |
| 1 |
| 2 |
∴Tn=3-(2n+3)(
| 1 |
| 2 |
点评:本题考查数列求和,错位相减法的应用,等比数列的判断,考查分析问题解决问题的能力.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
用反证法证明命题:“已知a、b∈N*,如果ab可被 5 整除,那么a、b 中至少有一个能被 5 整除”时,假设的内容应为( )
| A、a、b都能被5整除 |
| B、a、b都不能被5整除 |
| C、a、b不都能被5整除 |
| D、a不能被5整除 |
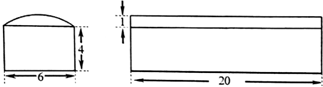
某校新校区建设在市二环路主干道旁,因安全需要,挖掘建设了一条人行地下通道,地下通道设计三视图中的主(正)视力(其中上部分曲线近似为抛物)和侧(左)视图如图(单位:m),则该工程需挖掘的总土方数为( )

| A、560m3 |
| B、540m3 |
| C、520m3 |
| D、500m3 |
 如图,已知PA,PB切⊙O于A,B两点,CD切⊙O于点E,交PA,PB于点C,D,若⊙O的半径为r,△PCD的周长为3r,则
如图,已知PA,PB切⊙O于A,B两点,CD切⊙O于点E,交PA,PB于点C,D,若⊙O的半径为r,△PCD的周长为3r,则