题目内容
已知函数f(x)=
,且f(1)=3.
(1)求证:函数f(x)在[
,+∞)上单调递增;
(2)设关于x的方程f(x)=x+b的两根为x1,x2,是否存在实数t,使得不等式2m2-t•m+4≥|x1-x2|对?b∈[2,
]及?m∈[
,2]恒成立?若存在,求实数t的取值范围;若不存在说明理由.
| 2x2+a |
| x |
(1)求证:函数f(x)在[
| ||
| 2 |
(2)设关于x的方程f(x)=x+b的两根为x1,x2,是否存在实数t,使得不等式2m2-t•m+4≥|x1-x2|对?b∈[2,
| 13 |
| 1 |
| 2 |
考点:导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:(1)由f(1)=3求得a值,然后求出函数的导函数,由导函数在[
,+∞)上大于等于0恒成立得答案;
(2)把f(x)的解析式代入f(x)=x+b,化为关于x的一元二次方程后求得|x1-x2|,再求出b∈[2,
]时|x1-x2|的最大为3.则问题转化为m∈[
,2]时2m2-tm+1≥0恒成立.然后分二次不等式对应的二次函数的对称轴在区间两侧和在区间内分类求最小值,由最小值大于等于0求解t的取值范围.
| ||
| 2 |
(2)把f(x)的解析式代入f(x)=x+b,化为关于x的一元二次方程后求得|x1-x2|,再求出b∈[2,
| 13 |
| 1 |
| 2 |
解答:
(1)证明:由f(x)=
,且f(1)=3.
得:2+a=3,解得a=1.
∴f(x)=
=2x+
.
f′(x)=2-
.
当x≥
时,f′(x)≥0.
∴函数f(x)在[
,+∞)上单调递增;
(2)解:由f(x)=x+b,得:
=x+b,化简:x2-bx+1=0.
|x1-x2|=
=
,
当b∈[2,
]时,|x1-x2|的最大为3.
不等式2m2-t•m+4≥|x1-x2|对?b∈[2,
]及?m∈[
,2]恒成立,
只需m∈[
,2]时,2m2-tm+4≥3恒成立.
也就是2m2-tm+1≥0恒成立.
函数y=2m2-tm+1的对称轴m=
.
当
≤
时,函数在[
,2]上单调递增,在m=
时取得最小值,
则只需要最小值大于等于0即可,即
-
+1≥0,即t≤3,结合t≤2得t≤2.
当
<
<2,即2<t<8时,函数最小值为:
,则有
≥0,
解得:-2
≤t≤2
,则2<t≤2
当
≥2,即t≥8时,函数在[
,2]上单调递减,在m=2取得最小值,
则只需要最小值大于等于03,
即18-3t+1≥0,解得t≤
,不符合.
综上:存在t≤2
,使得不等式2m2-t•m+4≥|x1-x2|对?b∈[2,
]及?m∈[
,2]恒成立.
| 2x2+a |
| x |
得:2+a=3,解得a=1.
∴f(x)=
| 2x2+1 |
| x |
| 1 |
| x |
f′(x)=2-
| 1 |
| x2 |
当x≥
| ||
| 2 |
∴函数f(x)在[
| ||
| 2 |
(2)解:由f(x)=x+b,得:
| 2x2+1 |
| x |
|x1-x2|=
| (x1+x2)2-4x1x2 |
| b2-4 |
当b∈[2,
| 13 |
不等式2m2-t•m+4≥|x1-x2|对?b∈[2,
| 13 |
| 1 |
| 2 |
只需m∈[
| 1 |
| 2 |
也就是2m2-tm+1≥0恒成立.
函数y=2m2-tm+1的对称轴m=
| t |
| 4 |
当
| t |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
则只需要最小值大于等于0即可,即
| 1 |
| 2 |
| t |
| 2 |
当
| 1 |
| 2 |
| t |
| 4 |
| 8-t2 |
| 8 |
| 8-t2 |
| 8 |
解得:-2
| 2 |
| 2 |
| 2 |
当
| t |
| 4 |
| 1 |
| 2 |
则只需要最小值大于等于03,
即18-3t+1≥0,解得t≤
| 19 |
| 3 |
综上:存在t≤2
| 2 |
| 13 |
| 1 |
| 2 |
点评:本题考查了利用导数研究函数的单调性,考查了数学转化思想方法,训练了利用函数的单调性求函数的最值,解答此题的关键在于转化思想方法的运用,是有一定难度题目.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 随机抽取100名高三学生的2014年省质检数学成绩,经数据处理后制作如图所示的频率分布直方图,那么,根据图形信息,可以推断出成绩在(80,100)之间的人数是( )
随机抽取100名高三学生的2014年省质检数学成绩,经数据处理后制作如图所示的频率分布直方图,那么,根据图形信息,可以推断出成绩在(80,100)之间的人数是( )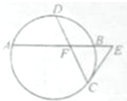 如图,已知圆中两条弦AB与CD相交于点F,且DF=CF=
如图,已知圆中两条弦AB与CD相交于点F,且DF=CF=
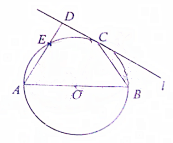 如图,圆O的直径AB=8,C为圆周上一点,BC=4,过C作圆的切线l,过A作直线l的垂线AD,D为垂足,AD与圆O交于点E,则线段DE的长为
如图,圆O的直径AB=8,C为圆周上一点,BC=4,过C作圆的切线l,过A作直线l的垂线AD,D为垂足,AD与圆O交于点E,则线段DE的长为