题目内容
19.如果函数f(x)对其定义域内的两个实数x1、x2,都满足不等式$f({\frac{{{x_1}+{x_2}}}{2}})<\frac{{f({x_1})+f({x_2})}}{2}$,则称函数f(x)在其定义域内具有性质M.给出下列函数:①$y=\sqrt{x}$;②y=x2;③y=2x;④y=log2x.其中具有性质M的是( )| A. | ①④ | B. | ②③ | C. | ③④ | D. | ①②③④ |
分析 由不等式$f({\frac{{{x_1}+{x_2}}}{2}})<\frac{{f({x_1})+f({x_2})}}{2}$可知:函数为下凸函数,画出图象即可判断出.
解答 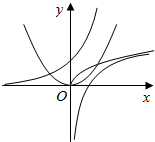 解:函数f(x)对其定义域内的任意两个实数x1,x2都满足不等式$f({\frac{{{x_1}+{x_2}}}{2}})<\frac{{f({x_1})+f({x_2})}}{2}$,则称函数f(x)在定义域上具有性质M,(为下凸函数).
解:函数f(x)对其定义域内的任意两个实数x1,x2都满足不等式$f({\frac{{{x_1}+{x_2}}}{2}})<\frac{{f({x_1})+f({x_2})}}{2}$,则称函数f(x)在定义域上具有性质M,(为下凸函数).
由函数的图象可知:②y=x2;③y=2x.其中具有性质M.
故选B.
点评 本题考查了下凸函数的性质,考查了数形结合思想方法与推理能力,属于中档题.

练习册系列答案
相关题目
9.已知变量x与y负相关,且由观测数据算得样本平均数$\overline x$=3,$\overline y$=3.5,则由该观测数据算得的线性回归方程可能是( )
| A. | $\stackrel{∧}{y}$=0.4x+2.3 | B. | $\stackrel{∧}{y}$=2x-2.4 | C. | $\stackrel{∧}{y}$=-2x+9.5 | D. | $\stackrel{∧}{y}$=-0.4x+4.4 |
10.设α,β,γ为两两不重合的平面,l,m,n为两两不重合的直线,给出下列四个命题,其中真命题有( )
①若m?α,n?β,α⊥β,则m⊥n;
②若m⊥α,n∥β且α∥β,则m⊥n;
③若α∥β,l?α,则l∥β;
④若α∩β=l,β∩γ=m,γ∩α=n,l∥γ,则m∥n.
①若m?α,n?β,α⊥β,则m⊥n;
②若m⊥α,n∥β且α∥β,则m⊥n;
③若α∥β,l?α,则l∥β;
④若α∩β=l,β∩γ=m,γ∩α=n,l∥γ,则m∥n.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.从长度分别位2、4、6、8、10的五条线段中,任取3条,则所得的3条线段中能组成三角形的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{10}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{10}$ |
8.已知数列{an}满足a1=2,an+1-an=-1(n∈N+),则此数列的通项an等于( )
| A. | n2+1 | B. | n+1 | C. | 1-n | D. | 3-n |
9.已知等差数列{an}的前n项和为Sn,a2=-2,S4=-4,若Sn取得最小值,则n的值为( )
| A. | n=2 | B. | n=3 | C. | n=2或n=3 | D. | n=4 |