题目内容

18．已知函数f（x）=2sin（$\frac{x}{4}$+2），如果存在实数x1，x2使得对任意的实数，都有f（x1）≤f（x2），则|x1-x2|的最小值是4π．

分析 先根据f（x1）≤f（x2）对任意实数x成立，进而可得到x1、x2是函数f（x）对应的最大、最小值的x，得到|x1-x2|一定是$\frac{T}{2}$的整数倍，然后求出函数f（x）=2sin（$\frac{x}{4}$+2）的最小正周期，根据|x1-x2|=n×$\frac{T}{2}$=4nπ可求出求出最小值．

解答 解：∵存在实数x1，x2使得对任意的实数，都有f（x1）≤f（x2），
∴x1、x2是函数f（x）对应的最小、最大值的x，
故|x1-x2|一定是$\frac{T}{2}$的整数倍；
∵函数f（x）=2sin（$\frac{x}{4}$+2）的最小正周期T=$\frac{2π}{\frac{1}{4}}$=8π，
∴|x1-x2|=n×$\frac{T}{2}$=4nπ（n＞0，且n∈Z），
∴|x1-x2|的最小值为4π；
故答案为：4π．

点评 本题考查了求正弦函数的图象与性质的应用问题，解题时应深刻理解题意，灵活应用基础知识，属于中档题．

练习册系列答案
相关题目
8．已知函数f（x）=cos（ωx+φ）（ω＞0，-π＜φ＜0）的最小正周期为π，且它的图象过点（$\frac{π}{6}$，$\frac{1}{2}$）．
（Ⅰ）求ω，φ的值；
（Ⅱ）求函数y=f（x）的单调增区间．
9．${log_2}\sqrt{2}+{log_2}\frac{{\sqrt{2}}}{2}$=0．
6．若圆锥的侧面展开图的圆心角为90°，半径为r，则该圆锥的全面积为（　　）
A．$\frac{π{r}^{2}}{16}$B．$\frac{3π{r}^{2}}{16}$C．$\frac{π{r}^{2}}{4}$D．$\frac{5π{r}^{2}}{16}$
13．在△ABC中，$\overrightarrow{AB}$=$\overrightarrow{m}$，$\overrightarrow{AC}$=$\overrightarrow{n}$，若点D满足$\overrightarrow{BD}$=2$\overrightarrow{DC}$，则$\overrightarrow{AD}$=（　　）
A．$\frac{1}{3}\overrightarrow{n}$+$\frac{2}{3}\overrightarrow{m}$B．$\frac{5}{3}$$\overrightarrow{m}$-$\frac{2}{3}\overrightarrow{n}$C．$\frac{2}{3}\overrightarrow{n}$-$\frac{1}{3}\overrightarrow{m}$D．$\frac{2}{3}\overrightarrow{n}$+$\frac{1}{3}\overrightarrow{m}$
3．求下列函数周期：
（1）y=|sinx|+sinx
（2）y=2sin（2x+$\frac{π}{3}$），x∈[-$\frac{π}{6}$，$\frac{π}{6}$]
（3）y=$\frac{cosx-2}{cosx-1}$
（4）y=2cos（2x+$\frac{π}{3}$），x∈R．
10．曲线f（x）=$\frac{-4}{\sqrt{3}（{e}^{x}+1）}$在点（0，f（0））处的切线方程为（　　）
A．x-$\sqrt{3}$y-2=0B．$\sqrt{3}$x+y-2=0C．x-$\sqrt{3}$y+2=0D．$\sqrt{3}$x+y+2=0
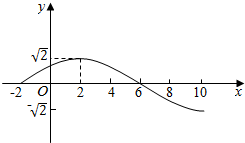7．已知在平行四边形ABCD中，$\overrightarrow{AC}$=$\overrightarrow{a}$，$\overrightarrow{BD}$=$\overrightarrow{b}$，则$\overrightarrow{AB}$=$\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$．
8．函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则f（x）=$\sqrt{2}$sin（$\frac{π}{8}$x+$\frac{π}{4}$）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网