题目内容
13.在△ABC中,$\overrightarrow{AB}$=$\overrightarrow{m}$,$\overrightarrow{AC}$=$\overrightarrow{n}$,若点D满足$\overrightarrow{BD}$=2$\overrightarrow{DC}$,则$\overrightarrow{AD}$=( )| A. | $\frac{1}{3}\overrightarrow{n}$+$\frac{2}{3}\overrightarrow{m}$ | B. | $\frac{5}{3}$$\overrightarrow{m}$-$\frac{2}{3}\overrightarrow{n}$ | C. | $\frac{2}{3}\overrightarrow{n}$-$\frac{1}{3}\overrightarrow{m}$ | D. | $\frac{2}{3}\overrightarrow{n}$+$\frac{1}{3}\overrightarrow{m}$ |
分析 根据向量减法的几何意义,便可由$\overrightarrow{BD}=2\overrightarrow{DC}$得,$\overrightarrow{AD}-\overrightarrow{AB}=2(\overrightarrow{AC}-\overrightarrow{AD})$,进行向量的数乘运算便可用$\overrightarrow{m},\overrightarrow{n}$表示出$\overrightarrow{AD}$.
解答 解:$\overrightarrow{BD}=2\overrightarrow{DC}$;
∴$\overrightarrow{AD}-\overrightarrow{AB}=2(\overrightarrow{AC}-\overrightarrow{AD})$;
∴$\overrightarrow{AD}=\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AC}$=$\frac{1}{3}\overrightarrow{m}+\frac{2}{3}\overrightarrow{n}$.
故选:D.
点评 考查向量减法的几何意义,以及向量的数乘运算.

练习册系列答案
相关题目
3.已知函数f(x)=|log0.5x|,若正实数m,n(m<n)满足f(m)=f(n),且f(x)在区间[m2,n]上的最大值为4,则n-m=( )
| A. | $\frac{3}{2}$ | B. | $\frac{15}{4}$ | C. | $\frac{63}{4}$ | D. | $\frac{255}{16}$ |
1.已知函数f(x)=x2-1g(10x+10),若0<b<1,则f(b)的值满足( )
| A. | f(b)>f(-$\frac{9}{10}$) | B. | f(b)>0 | C. | f(b)>f($\frac{3}{2}$) | D. | f(b)<f($\frac{3}{2}$) |
8.通过市场调查知某商品每件的市场价y(单位:圆)与上市时间x(单位:天)的数据如下:
根据上表数据,当a≠0时,下列函数:①y=ax+k;②y=ax2+bx+c;③y=alogmx中能恰当的描述该商品的市场价y与上市时间x的变化关系的是(只需写出序号即可)②.
| 上市时间x天 | 4 | 10 | 36 |
| 市场价y元 | 90 | 51 | 90 |
3.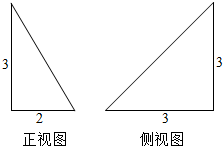 已知一个三棱锥的正视图,侧视图均为直角三角形,其形状及尺寸如图,则该三棱锥的俯视图的面积为( )
已知一个三棱锥的正视图,侧视图均为直角三角形,其形状及尺寸如图,则该三棱锥的俯视图的面积为( )
 已知一个三棱锥的正视图,侧视图均为直角三角形,其形状及尺寸如图,则该三棱锥的俯视图的面积为( )
已知一个三棱锥的正视图,侧视图均为直角三角形,其形状及尺寸如图,则该三棱锥的俯视图的面积为( )| A. | 3 | B. | 6 | C. | $\frac{9}{2}$或9 | D. | 3或6 |