题目内容

6．设f（x）＜0是定义在R上的奇函数，且f（2）＜0，当x＞0时，有$\frac{xf′（x）-f（x）}{{x}^{2}}$＜0恒成立，则不等式x2f（x）＞0的解集是（　　）
A．（-2，0）∪（2，+∞）B．（-2，0）∪（0，2）C．（-∞，-2）∪（2，+∞）D．（-∞，-2）∪（0，2）

分析 构造函数，通过$\frac{xf′（x）-f（x）}{{x}^{2}}$＜0化为[$\frac{f（x）}{x}$]′＜0；然后利用导函数的正负性，可判断函数y=$\frac{f（x）}{x}$在（0，+∞）内单调递减；再由f（2）=0，易得f（x）在（0，+∞）内的正负性；最后结合奇函数的图象特征，可得f（x）在（-∞，0）内的正负性．则x2f（x）＞0?f（x）＞0的解集即可求得．

解答 解：因为当x＞0时，有$\frac{xf′（x）-f（x）}{{x}^{2}}$＜0恒成立，即[$\frac{f（x）}{x}$]′＜0恒成立，
所以$\frac{f（x）}{x}$在（0，+∞）内单调递减．
因为f（2）=0，
所以在（0，2）内恒有f（x）＞0；在（2，+∞）内恒有f（x）＜0．
又因为f（x）是定义在R上的奇函数，
所以在（-∞，-2）内恒有f（x）＞0；在（-2，0）内恒有f（x）＜0．
又不等式x2f（x）＞0的解集，即不等式f（x）＞0的解集：（-∞，-2）∪（0，2）．
故选：D．

点评 本题主要考查了函数单调性与奇偶性的应用．在判断函数的单调性时，常可利用导函数来判断．属于中档题．

练习册系列答案
相关题目
16．在平面直角坐标系xOy中，抛物线y2=4x的焦点到其准线的距离为2．
17．已知M={x|y=$\sqrt{1-lo{g}_{2}x}$}，N={x|x2-2x-3＜0}，则M∩N=（　　）
A．（0，2）B．（-1，2]C．（0，2]D．（-1，3）
14．计算：（0.027）${\;}^{\frac{1}{3}}$-（6$\frac{1}{4}$）${\;}^{\frac{1}{2}}$+（2$\sqrt{2}$）${\;}^{-\frac{2}{3}}$+π0-3-1=-$\frac{31}{30}$．
1．把函数g（x）=sin（x-$\frac{π}{6}$）的图象向右平移$\frac{π}{6}$个单位可以得到函数f（x）的图象，则f（$\frac{π}{6}$）=（　　）
A．-$\frac{1}{2}$B．$\frac{\sqrt{3}}{2}$C．-1D．1
11．已知直线l：$\left\{\begin{array}{l}{x=5+\sqrt{3}t}\\{y=\sqrt{3}+t}\end{array}\right.$（t为参数），曲线C的坐标方程为ρ=6cosθ．
（1）将曲线C的极坐标方程化为直坐标方程；
（2）若点M（5，$\sqrt{3}$），直线l与曲线C的交点为A，B，求①|MA|•|MB|；②|MA|+|MB|的值；③|AB|的值；④||MA|-|MB||的值；
（3）若点M（8，2$\sqrt{3}$），直线l与曲线C的交点为A，B，求$\frac{1}{|MA|}$+$\frac{1}{|MB|}$的值．
18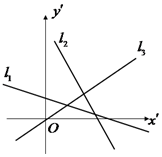．如图，在平面直角坐标系中有三条直线l1，l2，l3，其对应的斜率分别为k1，k2，k3，则下面选项中正确的是（　　）
A．k3＞k1＞k2B．k1-k2＜0C．k2•k3＞0D．k3＞k2＞k1
15．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左焦点为F，离心率为$\frac{1}{2}$，直线与椭圆相交于A，B两点，当AB⊥x轴时，△ABF的周长最大值为8．
（1）求椭圆的方程；
（2）若直线过点M（-4，0），求当△ABF面积最大时直线AB的方程．
16．已知函数f（x）=x|x|-2x，则下列结论正确的是（　　）
A．f（x）是偶函数，单调递增区间是（0，+∞）B．f（x）是偶函数，单调递减区间是（-∞，1）
C．f（x）是奇函数，单调递增区间是（-∞，0）D．f（x）是奇函数，单调递减区间是（-1，1）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网