题目内容
若关于x的不等式x2-4x＜mx的解集为{x|0＜x＜2}，则m= ．
考点：一元二次不等式的解法
专题：不等式的解法及应用
分析：把不等式x2-4x＜mx化为x2-（m+4）x＜0，由解集得出不等式对应的方程的两根，由根与系数的关系求出m的值．
解答：
解：∵不等式x2-4x＜mx可化为
x2-（m+4）x＜0，
且解集为{x|0＜x＜2}；
∴方程x2-（m+4）x=0的两个根为0、2，
∴m+4=2；
∴m=-2．
故答案为：-2．
x2-（m+4）x＜0，
且解集为{x|0＜x＜2}；
∴方程x2-（m+4）x=0的两个根为0、2，
∴m+4=2；
∴m=-2．
故答案为：-2．
点评：本题考查了一元二次方程与一元二次不等式之间的关系与应用问题，解题时应灵活地运用二者之间的关系进行解答，是基础题．
练习册系列答案
导学全程练创优训练系列答案
相关题目
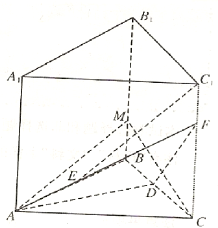如图，在直三棱柱ABC-A1B1C1中，D、E分别是棱BC、AB的中点，点F在棱CC1上，已知AB=AC，AA1=3，BC=CF=2若z=
，则
=（ ）
| 1-2i |
| i |
. |
| z |
| A、-2-i | B、-2+i |
| C、1+i | D、1-i |