题目内容
随机地向半圆0＜y＜
（a为正常数）内掷一点，点落在半圆内任何区域的概率与区域的面积成正比，则原点与该点的连线与x轴的夹角小于
的概率为 ．
| 2ax-x2 |
| π |
| 4 |
考点：几何概型
专题：概率与统计
分析：用积分的办法解比较麻烦，利用几何方法解相对简单．
解答：
解：根据条件，可知半圆如图，原点与该点的连线与x轴的夹角小于
的点应在S1区域内，
S1的面积和半圆面积的比值即为落在S1内的概率
S1=S△AOC+S扇形ABC=
+
，
半圆面积是S半圆=
，
=
+
．
故答案为：
+
．
| π |
| 4 |
S1的面积和半圆面积的比值即为落在S1内的概率
S1=S△AOC+S扇形ABC=
| a2 |
| 2 |
| πa2 |
| 4 |
半圆面积是S半圆=
| πa2 |
| 2 |
| S1 |
| S半圆 |
| 1 |
| 2 |
| 1 |
| π |
故答案为：
| 1 |
| 2 |
| 1 |
| π |
点评：本题主要考察概率问题的几何运用，运用图形解决方便快捷，最主要的是要清楚S1的面积和半圆面积的比值即为落在S1内的概率，本题属于基础题．
练习册系列答案
相关题目
命题“对任意x∈R，总有x2+1＞0”的否定是（ ）
| A、“对任意x∉R，总有x2+1＞0” |
| B、“对任意x∈R，总有x2+1≤0” |
| C、“存在x∈R，使得x2+1＞0” |
| D、“存在x∈R，使得x2+1≤0” |
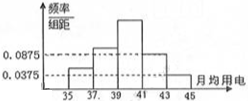某乡镇供电所为了调查农村居民用电量情况，随机抽取了500户居民去年的用电量（单位：kw/h），将所得数据整理后，画出频率分布直方图如图．其中直方图从左到右前3个小矩形的面积之比为1：2：3．过函数y=sinx图象上一点O（0，0）作切线，则切线方程为（ ）
| A、y=x | B、y=0 |
| C、y=x+1 | D、y=-x+1 |