题目内容

13．若正数x，y满足4x+9y=xy，则x+y的最小值为（　　）
A．16B．20C．25D．36

分析 变形已知式子可得$\frac{9}{x}$+$\frac{4}{y}$=1，整体代入可得x+y=（x+y）（$\frac{9}{x}$+$\frac{4}{y}$）=13+$\frac{9y}{x}$+$\frac{4x}{y}$，由基本不等式可得．

解答 解：∵正数x，y满足4x+9y=xy，
∴$\frac{4x+9y}{xy}$=1，即$\frac{9}{x}$+$\frac{4}{y}$=1，
∴x+y=（x+y）（$\frac{9}{x}$+$\frac{4}{y}$）
=13+$\frac{9y}{x}$+$\frac{4x}{y}$≥13+2$\sqrt{\frac{9y}{x}•\frac{4x}{y}}$=25，
当且仅当$\frac{9y}{x}$=$\frac{4x}{y}$即2x=3y时取等号，
结合$\frac{9}{x}$+$\frac{4}{y}$=1可解得x=15且y=10，
故选：C．

点评 本题考查基本不等式求最值，变形并整体代入化已知式子为可用基本不等式的形式是解决问题的关键，属中档题．

练习册系列答案
相关题目
11．计算下列各排列数：
（1）a，b，c，d，e中取出4个元素的排列中，a不在首位的所有排列；
（2）a，b，c，d，e中取出4个元素的排列中，a不在首位且b不在末位的所有排列．
4．已知函数f（x）=m-|2x+1|-|2x-3|在R上存在零点．
（1）求实数m的取值范围；
（2）当m为最小值时，若$\frac{1}{m\sqrt{a}}$+$\frac{1}{2m\sqrt{b}}$+$\frac{1}{3m\sqrt{c}}$=1，求证：$\frac{1}{9}$$\sqrt{a}$+$\frac{2}{9}$$\sqrt{b}$+$\frac{1}{3}$$\sqrt{c}$≥$\frac{1}{4}$．
1．设M为平面上以A（4，1），B（-1，-6），C（-3，2）三点为顶点的三角形区域（包括内部和边界），当点（x，y）在M上变化时，z=4x-3y的取值范围是（　　）
A．[-18，13]B．[0，14]C．[13，14]D．[-18，14]
8．设P（x，y）满足$\left\{\begin{array}{l}{x-2y≥0}\\{x+2y≥0}\end{array}\right.$，且P点到两直线x-2y=0，x+2y=0距离之和不大于$\sqrt{5}$，则x-y的最大值为$\frac{15}{4}$．
18．已知函数f（x）=a•（$\frac{1}{3}$）x+bx2+cx（a∈R，b≠0，c∈R），若{x|f（x）=0}={x|f（f（x））=0}≠∅，则实数c的取值范围为[0，4）．
5．15名选举人对5名侯选人进行无记名投票选举，若选举人可以投一个至五个候选人的票，也可以弃权，则不同的选举方法共有（　　）
A．215种B．275种C．25种D．225种
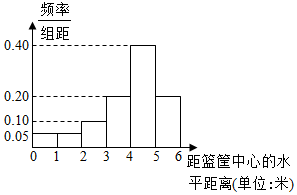2．某篮球队对篮球运动员的篮球技能进行统计研究，针对篮球运动员在投篮命中时，运动员在篮筐中心的水平距离这项指标，对某运动员进行了若干场次的统计，依据统计结果绘制如下频率分布直方图：
（Ⅰ）依据频率分布直方图估算该运动员投篮命中时，他到篮筐中心的水平距离的中位数；
（Ⅱ）若从该运动员投篮命中时，他到篮筐中心的水平距离为2到5米的这三组中，用分层抽样的方法抽取7次成绩（单位：米，运动员投篮命中时，他到篮筐中心的水平距离越远越好），并从抽到的这7次成绩中随机抽取2次．规定：这2次成绩均来自到篮筐中心的水平距离为4到5米的这一组，记1分，否则记0分．求该运动员得1分的概率．
3．已知虚数1+2i是方程x2+ax+b=0（a，b∈R）的一个根，则a+b=3．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网