题目内容
已知2sin(x+
)=1,则cos(x+π)=( )
| π |
| 2 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:已知等式利用诱导公式化简求出cosx的值,所求式子利用诱导公式化简后将cosx的值代入计算即可求出值.
解答:
解:∵2sin(x+
)=2cosx=1,即cosx=
,
∴cos(x+π)=-cosx=-
.
故选:B.
| π |
| 2 |
| 1 |
| 2 |
∴cos(x+π)=-cosx=-
| 1 |
| 2 |
故选:B.
点评:此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键.

练习册系列答案
相关题目
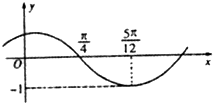 从函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<
从函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<| π |
| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
点P(a,10)与圆(x-1)2+(y-1)2=2的位置关系是( )
| A、在圆外 | B、在圆内 |
| C、在圆上 | D、与a的值有关 |
等比数列{an}满足a2+a4=20,a3+a5=40,则公比q=( )
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |
要得到函数y=sin(2x+
)的图象,只要将函数y=cos2x的图象( )
| π |
| 4 |
A、向左平移
| ||
B、向右平移
| ||
C、向右平移
| ||
D、向左平移
|
定积分
xdx等于( )
| ∫ | 3 0 |
A、
| ||
| B、9 | ||
| C、8 | ||
| D、3 |
已知数列
,
,
,
,…,那么0.98,0.96,0.94中属于该数列中某一项值的应当有( )
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| 4 |
| 5 |
| A、0个 | B、1个 | C、2个 | D、3个 |