题目内容
13.已知正三棱锥P-ABC,点P,A,B,C都在半径为1的球面上,若PA,PB,PC两两互相垂直,则球心到截面ABC的距离为$\frac{1}{3}$.分析 先利用正三棱锥的特点,将球的内接三棱锥问题转化为球的内接正方体问题,从而将所求距离转化为正方体中,中心到截面的距离问题,利用等体积法可实现此计算.
解答 解:∵正三棱锥P-ABC,PA,PB,PC两两垂直,
∴此正三棱锥的外接球即以PA,PB,PC为三边的正方体的外接球O,
∵球O的半径为1,
∴正方体的边长为$\frac{2\sqrt{3}}{3}$,即PA=PB=PC=$\frac{2\sqrt{3}}{3}$,
球心到截面ABC的距离即正方体中心到截面ABC的距离,
设P到截面ABC的距离为h,则正三棱锥P-ABC的体积V=$\frac{1}{3}$S△ABC×h=$\frac{1}{3}$S△PAB×PC=$\frac{1}{3}×\frac{1}{2}×(\frac{2\sqrt{3}}{3})^{3}$,
△ABC为边长为$\frac{2\sqrt{6}}{3}$的正三角形,S△ABC=$\frac{\sqrt{3}}{4}$×($\frac{2\sqrt{6}}{3}$)2=$\frac{2\sqrt{3}}{3}$,
∴h=$\frac{2}{3}$,
∴球心(即正方体中心)O到截面ABC的距离为$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 本题主要考球的内接三棱锥和内接正方体间的关系及其相互转化,棱柱的几何特征,球的几何特征,点到面的距离问题的解决技巧,有一定难度,属中档题.

练习册系列答案
相关题目
3.若{1,a,$\frac{b}{a}$}={0,a2,a+b},则a2009+b2009的值为( )
| A. | 0 | B. | 1 | C. | -1 | D. | 1或-1 |
1.直线l的参数方程是$\left\{\begin{array}{l}{x=1+2t}\\{y=2-t}\end{array}\right.$(t∈R),则l的斜率为( )
| A. | -1 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | 2 |
5.已知 a1=3,a2=6,且 an+2=an+1-an,则a2011=( )
| A. | 3 | B. | -3 | C. | 6 | D. | -6 |
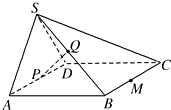 如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD,四边形ABCD为正方形,且P为AD的中点,Q为SB的中点.
如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD,四边形ABCD为正方形,且P为AD的中点,Q为SB的中点.