题目内容
已知函数f(x)=(2-x)ex,g(x)=(x2+ax-2a-3)ex,求证:当a≥-3时,一定存在x1、x2∈[0,5],使得f(x1)-g(x2)≥0.
考点:利用导数求闭区间上函数的最值,函数恒成立问题
专题:函数的性质及应用,导数的综合应用
分析:求函数的导数,利用导数求函数f(x)和g(x)在[0,5]上的最值,只要证明f(x)max≥g(x)max.即可得到证明结论.
解答:
解:∵f(x)=(2-x)ex,
∴f'(x)=-xex+(2-x)ex=(2-2x)ex,
由f'(x)<0得x>1,此时函数单调递增,
由f'(x)>0得x<1,此时函数单调递减,
∴当x=1时,函数取得最大值f(1)=e,
∴当x∈[0,5]时,函数取得最大值f(1)=e.
∵g(x)=(x2+ax-2a-3)ex,
∴g'(x)=(2x+a)ex+(x2+ax-2a-3)ex=[x2+(a+2)x-a-3]ex=(x-1)(x+a+3)ex,
由g'(x)=(x-1)(x+a+3)ex=0,
得x=1或x=-a-3,
∵a≥-3,
∴-a-3≤0,
∴当1≤x≤5时,g'(x)≥0此时函数单调递增,
当0≤x≤1时,g'(x)≤0此时函数单调递减.
∴当x=1时,函数g(x)取得极小值同时也是最小值为g(1)=(-a-2)e.
即函数g(x)在[0,5]上的最小值为g(1)=(-a-2)e.
∵当x∈[0,5],f(x)≤e,g(x)≥(-a-2)e.
∴当a≥-3时,(-a-2)e≤e,
即f(x)max≥g(x)max.
即当a≥-3时,一定存在x1、x2∈[0,5],使得f(x1)≥g(x2)成立,
即f(x1)-g(x2)≥0.成立.
∴f'(x)=-xex+(2-x)ex=(2-2x)ex,
由f'(x)<0得x>1,此时函数单调递增,
由f'(x)>0得x<1,此时函数单调递减,
∴当x=1时,函数取得最大值f(1)=e,
∴当x∈[0,5]时,函数取得最大值f(1)=e.
∵g(x)=(x2+ax-2a-3)ex,
∴g'(x)=(2x+a)ex+(x2+ax-2a-3)ex=[x2+(a+2)x-a-3]ex=(x-1)(x+a+3)ex,
由g'(x)=(x-1)(x+a+3)ex=0,
得x=1或x=-a-3,
∵a≥-3,
∴-a-3≤0,
∴当1≤x≤5时,g'(x)≥0此时函数单调递增,
当0≤x≤1时,g'(x)≤0此时函数单调递减.
∴当x=1时,函数g(x)取得极小值同时也是最小值为g(1)=(-a-2)e.
即函数g(x)在[0,5]上的最小值为g(1)=(-a-2)e.
∵当x∈[0,5],f(x)≤e,g(x)≥(-a-2)e.
∴当a≥-3时,(-a-2)e≤e,
即f(x)max≥g(x)max.
即当a≥-3时,一定存在x1、x2∈[0,5],使得f(x1)≥g(x2)成立,
即f(x1)-g(x2)≥0.成立.
点评:本题主要考查函数最值和函数导数之间的关系,利用导数求出函数的最值是解决本题的关键,将不等式f(x1)-g(x2)≥0.转化为求f(x)max≥g(x)max.是解决本题的突破点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
运行如图所示的程序框图,则输出S的值为( )


| A、8 | B、4 | C、3 | D、-2 |
 如图,四边形ABCD与BDEF均为菱形,设AC与BD相交于点O,若∠DAB=∠DBF=60°,且FA=FC.
如图,四边形ABCD与BDEF均为菱形,设AC与BD相交于点O,若∠DAB=∠DBF=60°,且FA=FC.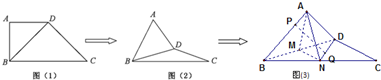 在直角梯形ABCD中,AD∥BC,
在直角梯形ABCD中,AD∥BC,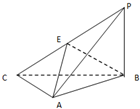 如图,三棱锥P-ABC中,PA⊥平面ABC,PB=BC=CA=4,∠BCA=90°,E为PC中点.
如图,三棱锥P-ABC中,PA⊥平面ABC,PB=BC=CA=4,∠BCA=90°,E为PC中点.