题目内容
已知{an}是等比数列,且a2=3,a4=27
(1)求数列{an}的通项公式;
(2)令bn=|an|,求{bn}的前n项的和Sn.
(1)求数列{an}的通项公式;
(2)令bn=|an|,求{bn}的前n项的和Sn.
考点:数列的求和,等比数列的性质
专题:等差数列与等比数列
分析:(1)由已知条件,利用等比数列的通项公式列出方程组,求出公比和首项,由此能求出数列{an}的通项公式.
(2)由(1)得到bn=|an|=3n-1,由此能求出{bn}的前n项和.
(2)由(1)得到bn=|an|=3n-1,由此能求出{bn}的前n项和.
解答:
解:(1)∵{an}是等比数列,且a2=3,a4=27,
∴
,
解得
,或
,
当
时,an=3n-1;
当
时,an=(-1)•(-3)n-1=-(-3)n-1.
∴q=3时,an=3n-1;q=-3时,an=-(-3)n-1.
(2)∵q=3时,an=3n-1,q=-3时,an=-(-3)n-1,
∴bn=|an|=3n-1,
∴{bn}是首项为1,公比为3的等比数列,
∴Sn=
=
.
∴
|
解得
|
|
当
|
当
|
∴q=3时,an=3n-1;q=-3时,an=-(-3)n-1.
(2)∵q=3时,an=3n-1,q=-3时,an=-(-3)n-1,
∴bn=|an|=3n-1,
∴{bn}是首项为1,公比为3的等比数列,
∴Sn=
| 1×(1-3n) |
| 1-3 |
| 3n-1 |
| 2 |
点评:本题考查数列的通项公式和前n项和公式的求法,是中档题,解题时要熟练掌握等比数列的性质.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案
相关题目
条件p:-2<x<4,条件q:(x+2)(x+a)<0;若p是q的充分而不必要条件,则a的取值范围是( )
| A、(4,+∞) |
| B、(-∞,-4) |
| C、(-∞,-4] |
| D、[-4,+∞) |
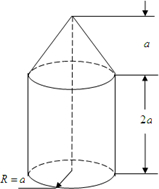 图示是一个几何体的直观图,画出它的三视图.
图示是一个几何体的直观图,画出它的三视图. 在三棱锥P-ABC中,侧棱长均为
在三棱锥P-ABC中,侧棱长均为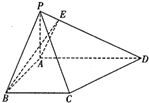 在四棱锥P-ABCD中,底面ABCD是一直角梯,∠BAD=90°,AD∥BC,AB=BC=a,AD=2a,PA⊥底面ABCD,PD与底面成30°角.
在四棱锥P-ABCD中,底面ABCD是一直角梯,∠BAD=90°,AD∥BC,AB=BC=a,AD=2a,PA⊥底面ABCD,PD与底面成30°角.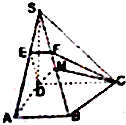 在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,S D=
在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,S D=