题目内容
已知等差数列{an}的公差大于0,且a3,a5是方程x2-14x+45=0的两根,数列{bn}的前n项和为Sn,且Sn=
(n∈N﹡).
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)记cn=an•bn,比较cn+1与cn的大小;
(Ⅲ)记cn=an•bn求数列{cn}的前n项和Tn.
| 1-bn |
| 2 |
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)记cn=an•bn,比较cn+1与cn的大小;
(Ⅲ)记cn=an•bn求数列{cn}的前n项和Tn.
考点:数列的求和,等差数列的通项公式,等比数列的通项公式
专题:综合题,等差数列与等比数列
分析:(Ⅰ)求出数列{an}的公差,即可求其通项,判断{bn}是等比数列,即可求{bn}通项公式;
(Ⅱ)求出cn=an•bn,利用作差法,即可比较cn+1与cn的大小;
(Ⅲ)利用错位相减法即可求得{cn}的前n项和Tn.
(Ⅱ)求出cn=an•bn,利用作差法,即可比较cn+1与cn的大小;
(Ⅲ)利用错位相减法即可求得{cn}的前n项和Tn.
解答:
解:(Ⅰ)方程x2-14x+45=0的两根是5,9.
∵等差数列{an}的公差大于0,且a3,a5是方程x2-14x+45=0的两根,
∴a3=5,a5=9,
∴d=2,
∴an=5+2(n-5)=2n-1;
当n≥2,bn=Sn-Sn-1=
(bn-1-bn),
∴bn=
bn-1,
∵bn=
,
∴数列{bn}是以
为首项,
为公比的等比数列,
∴bn=
;
(Ⅱ)cn=an•bn=
,
∴cn+1-cn=
-
=
,
∴n=1时,cn+1=cn,n≥时,cn+1<cn;
(Ⅲ)cn=an•bn=
,
∴Tn=c1+c2+c3+…+cn=
+3•3-2+5•3-3+…+(2n-1)•3-n①,
Tn=3-2+3•3-3+5•3-4+…+(2n-1)•3-n-1②,
①-②整理可得,Tn=1-n•3-n.
∵等差数列{an}的公差大于0,且a3,a5是方程x2-14x+45=0的两根,
∴a3=5,a5=9,
∴d=2,
∴an=5+2(n-5)=2n-1;
当n≥2,bn=Sn-Sn-1=
| 1 |
| 2 |
∴bn=
| 1 |
| 3 |
∵bn=
| 1 |
| 3 |
∴数列{bn}是以
| 1 |
| 3 |
| 1 |
| 3 |
∴bn=
| 1 |
| 3n |
(Ⅱ)cn=an•bn=
| 2n-1 |
| 3n |
∴cn+1-cn=
| 2n+1 |
| 3n+1 |
| 2n-1 |
| 3n |
| 4(1-n) |
| 3n+1 |
∴n=1时,cn+1=cn,n≥时,cn+1<cn;
(Ⅲ)cn=an•bn=
| 2n-1 |
| 3n |
∴Tn=c1+c2+c3+…+cn=
| 1 |
| 3 |
| 1 |
| 3 |
①-②整理可得,Tn=1-n•3-n.
点评:本题考查等差、等比数列的通项公式及数列求和,考查错位相减法对数列求和,属于中档题.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
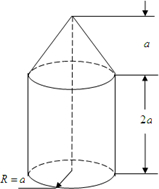 图示是一个几何体的直观图,画出它的三视图.
图示是一个几何体的直观图,画出它的三视图.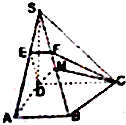 在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,S D=
在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,S D=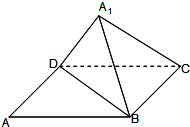 如图,已知矩形ABCD中,AB=10,BC=6,将矩形沿对角线BD把△ABD折起,使A移到A1点,且A1在平面BCD上的射影O恰好在CD上.
如图,已知矩形ABCD中,AB=10,BC=6,将矩形沿对角线BD把△ABD折起,使A移到A1点,且A1在平面BCD上的射影O恰好在CD上.