题目内容
 如图,四边形ABCD与BDEF均为菱形,设AC与BD相交于点O,若∠DAB=∠DBF=60°,且FA=FC.
如图,四边形ABCD与BDEF均为菱形,设AC与BD相交于点O,若∠DAB=∠DBF=60°,且FA=FC.(1)求证:FC∥平面EAD;
(2)求二面角A-FC-B的余弦值.
考点:与二面角有关的立体几何综合题,直线与平面平行的判定
专题:综合题,空间位置关系与距离,空间角
分析:(1)因为四边形ABCD与BDEF均为菱形,所以AD∥BC,DE∥BF,可得平面FBC∥平面EAD,由此能够证明FC∥平面EAD;
(2)证明FO⊥平面ABCD.由OA,OB,OF两两垂直,建立空间直角坐标系O-xyz.设AB=2.因为四边形ABCD为菱形,∠DAB=60°,则BD=2,求得平面BFC、平面AFC的法向量,由此能求出二面角A-FC-B的余弦值.
(2)证明FO⊥平面ABCD.由OA,OB,OF两两垂直,建立空间直角坐标系O-xyz.设AB=2.因为四边形ABCD为菱形,∠DAB=60°,则BD=2,求得平面BFC、平面AFC的法向量,由此能求出二面角A-FC-B的余弦值.
解答:
 (1)证明:因为四边形ABCD与BDEF均为菱形,
(1)证明:因为四边形ABCD与BDEF均为菱形,
所以AD∥BC,DE∥BF.
因为AD?平面FBC,DE?平面FBC,
所以AD∥平面FBC,DE∥平面FBC…(2分)
又AD∩DE=D,AD?平面EAD,DE?平面EAD,
所以平面FBC∥平面EAD
又FC?平面FBC,
所以FC∥平面EAD…(4分)
(2)解:连接FO、FD,则
因为四边形BDEF为菱形,且∠DBF=60°,
所以△DBF为等边三角形,
因为O为BD中点.所以FO⊥BD,
又因为O为AC中点,且FA=FC,
所以AC⊥FO
又AC∩BD=O,所以FO⊥平面ABCD….(6分)
由OA,OB,OF两两垂直,建立如图所示的空间直角坐标系O-xyz
设AB=2,因为四边形ABCD为菱形,∠DAB=60°,则BD=2,OB=1,OA=OF=
,
所以O(0,0,0),A(
,0,0),B(0,1,0),C(-
,0,0),F(0,0,
)…..(8分)
所以
=(
,0,
),
=(
,1,0),
设平面BFC的一个法向量为
=(x,y,z),
则有
,令x=1,则
=(1,-
,1)
因为BD⊥平面AFC,所以平面AFC的一个法向量为
=(0,1,0)….(10分)
因为二面角A-FC-B为锐二面角,设二面角的平面角为θ
则cosθ=|
|=
,
所以二面角A-FC-B的余弦值为
…(12分)
 (1)证明:因为四边形ABCD与BDEF均为菱形,
(1)证明:因为四边形ABCD与BDEF均为菱形,所以AD∥BC,DE∥BF.
因为AD?平面FBC,DE?平面FBC,
所以AD∥平面FBC,DE∥平面FBC…(2分)
又AD∩DE=D,AD?平面EAD,DE?平面EAD,
所以平面FBC∥平面EAD
又FC?平面FBC,
所以FC∥平面EAD…(4分)
(2)解:连接FO、FD,则
因为四边形BDEF为菱形,且∠DBF=60°,
所以△DBF为等边三角形,
因为O为BD中点.所以FO⊥BD,
又因为O为AC中点,且FA=FC,
所以AC⊥FO
又AC∩BD=O,所以FO⊥平面ABCD….(6分)
由OA,OB,OF两两垂直,建立如图所示的空间直角坐标系O-xyz
设AB=2,因为四边形ABCD为菱形,∠DAB=60°,则BD=2,OB=1,OA=OF=
| 3 |
所以O(0,0,0),A(
| 3 |
| 3 |
| 3 |
所以
| CF |
| 3 |
| 3 |
| CB |
| 3 |
设平面BFC的一个法向量为
| n |
则有
|
| n |
| 3 |
因为BD⊥平面AFC,所以平面AFC的一个法向量为
| OB |
因为二面角A-FC-B为锐二面角,设二面角的平面角为θ
则cosθ=|
| ||||
|
|
| ||
| 5 |
所以二面角A-FC-B的余弦值为
| ||
| 5 |
点评:本题考查直线与平面垂直、直线与平面平行的证明,考查二面角的余弦值的求法,考查学生分析解决问题的能力,注意向量法的合理运用.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
若不等式2x>x2+a对于一切x∈[-2,3]恒成立,则实数a的取值范围( )
| A、(-∞,-8) |
| B、(-∞,-3) |
| C、(-∞,1) |
| D、(-8,-∞) |
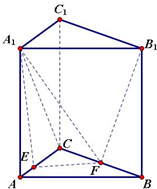 如图在三棱柱ABC-A1B1C1中,各侧棱都垂直于底面且地面为等腰直角三角形,∠ACB=90°,AC=BC=4,AA1=4,E,F分别在AC,BC上,且CE=3,CF=2,求几何体EFC-A1B1C1的体积.
如图在三棱柱ABC-A1B1C1中,各侧棱都垂直于底面且地面为等腰直角三角形,∠ACB=90°,AC=BC=4,AA1=4,E,F分别在AC,BC上,且CE=3,CF=2,求几何体EFC-A1B1C1的体积. 在三棱锥P-ABC中,侧棱长均为
在三棱锥P-ABC中,侧棱长均为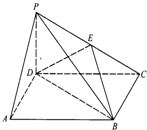 如图,四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是正方形,PD=AB=2,E为PC中点.
如图,四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是正方形,PD=AB=2,E为PC中点.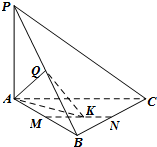 如图,在三棱锥P-ABC中,直线PA⊥平面ABC,且∠ABC=90°,又点Q,M,N分别是线段PB,AB,BC的中点,且点K是线段MN上的动点.
如图,在三棱锥P-ABC中,直线PA⊥平面ABC,且∠ABC=90°,又点Q,M,N分别是线段PB,AB,BC的中点,且点K是线段MN上的动点.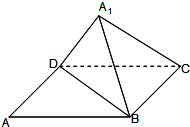 如图,已知矩形ABCD中,AB=10,BC=6,将矩形沿对角线BD把△ABD折起,使A移到A1点,且A1在平面BCD上的射影O恰好在CD上.
如图,已知矩形ABCD中,AB=10,BC=6,将矩形沿对角线BD把△ABD折起,使A移到A1点,且A1在平面BCD上的射影O恰好在CD上.