题目内容
已知函数f(x)=
(ax-a-x)(a>0,且a≠1),当x∈[-1,1]时,f(x)≥b恒成立,求b的取值范围.
| a |
| a2-1 |
考点:函数恒成立问题
专题:函数的性质及应用
分析:由函数单调性的定义得到函数在[-1,1]上为增函数,然后求得f(-1)的值得答案.
解答:
解:设-1≤x1<x2≤1,
则f(x1)-f(x2)=
(ax1-a-x1-ax2+a-x2)
=
(ax1-ax2+
-
)
=
(ax1-ax2+
)
=
(ax1-ax2)(1+
).
若a>1,
>0,ax1<ax2,1+
>0,
此时f(x1)-f(x2)<0,f(x1)<f(x2).
f(x)在[-1,1]上为增函数,
若0<a<1,
<0,ax1>ax2,1+
>0,
此时f(x1)-f(x2)<0,f(x1)<f(x2).
f(x)在[-1,1]上为增函数,
综上,对于a>0,且a≠1,当x∈[-1,1]时,f(x)为增函数.
∴当x∈[-1,1]时,要使f(x)≥b恒成立,
则b≤f(-1)=
(a-1-a)=-1.
∴b的取值范围是(-∞,-1).
则f(x1)-f(x2)=
| a |
| a2-1 |
=
| a |
| a2-1 |
| 1 |
| ax2 |
| 1 |
| ax1 |
=
| a |
| a2-1 |
| ax1-ax2 |
| ax1ax2 |
=
| a |
| a2-1 |
| 1 |
| ax1ax2 |
若a>1,
| a |
| a2-1 |
| 1 |
| ax1ax2 |
此时f(x1)-f(x2)<0,f(x1)<f(x2).
f(x)在[-1,1]上为增函数,
若0<a<1,
| a |
| a2-1 |
| 1 |
| ax1ax2 |
此时f(x1)-f(x2)<0,f(x1)<f(x2).
f(x)在[-1,1]上为增函数,
综上,对于a>0,且a≠1,当x∈[-1,1]时,f(x)为增函数.
∴当x∈[-1,1]时,要使f(x)≥b恒成立,
则b≤f(-1)=
| a |
| a2-1 |
∴b的取值范围是(-∞,-1).
点评:本题考查恒成立问题,考查了函数的性质,训练了分类讨论的数学思想方法,是中档题.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
设函数f(x)的定义域为D,如果存在正实数k,对于任意x∈D,都有x+k∈D,且f(x+k)>f(x)恒成立,则称函数f(x)为D上的“k型增函数”,已知函数f(x)是定义在R上的奇函数,且当x>0时,f(x)=|x-a|-2a,若f(x)为R上的“2014型增函数”,则实数a的取值范围是( )
| A、a<-1007 | ||
| B、a<1007 | ||
C、a<
| ||
D、a<-
|
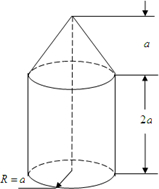 图示是一个几何体的直观图,画出它的三视图.
图示是一个几何体的直观图,画出它的三视图.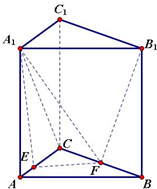 如图在三棱柱ABC-A1B1C1中,各侧棱都垂直于底面且地面为等腰直角三角形,∠ACB=90°,AC=BC=4,AA1=4,E,F分别在AC,BC上,且CE=3,CF=2,求几何体EFC-A1B1C1的体积.
如图在三棱柱ABC-A1B1C1中,各侧棱都垂直于底面且地面为等腰直角三角形,∠ACB=90°,AC=BC=4,AA1=4,E,F分别在AC,BC上,且CE=3,CF=2,求几何体EFC-A1B1C1的体积. 在三棱锥P-ABC中,侧棱长均为
在三棱锥P-ABC中,侧棱长均为