题目内容
16.设f'(x)是函数y=f(x)的导数,f''(x)是f'(x)的导数,若方程f''(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.已知:任何三次函数既有拐点,又有对称中心,且拐点就是对称中心.设$f(x)=\frac{1}{3}{x^3}-2{x^2}+\frac{8}{3}x+2$,数列{an}的通项公式为an=n-1007,则$\sum_{i=1}^{2017}{f({a_i})}$=( )| A. | 2017 | B. | 2018 | C. | 8068 | D. | 4034 |
分析 由题意对已知函数求两次导数可得f′′(x)=2x-4,由题意可得函数的图象关于点(2,2)对称,即f(x)+f(4-x)=2,由数列{an}的通项公式分析可得{an}为等差数列,且a1+a2017=a2+a2016=…=2a1009=4,而$\sum_{i=1}^{2017}{f({a_i})}$=f(a1)+f(a2)+…+f(a2016)+f(a2017),结合f(x)+f(4-x)=2,计算可得答案.
解答 解:根据题意,三次函数$f(x)=\frac{1}{3}{x^3}-2{x^2}+\frac{8}{3}x+2$,
则f′(x)=x2-4x+$\frac{8}{3}$,
则f′′(x)=2x-4,
若f′′(x)=2x-4=0,则有x=2,
又由$f(x)=\frac{1}{3}{x^3}-2{x^2}+\frac{8}{3}x+2$,则f(2)=2,
即(2,2)是三次函数$f(x)=\frac{1}{3}{x^3}-2{x^2}+\frac{8}{3}x+2$的对称中心,
则有f(x)+f(4-x)=4,
数列{an}的通项公式为an=n-1007,为等差数列,
则有a1+a2017=a2+a2016=…=2a1009=4
则$\sum_{i=1}^{2017}{f({a_i})}$=f(a1)+f(a2)+…+f(a2016)+f(a2017)
=f(a1)+f(a2017)+f(a2)+f(a2016)+…+f(a1008)+f(a1010)+f(a1009)
=4×1008+2=4034;
故选:D.
点评 本题考查函数的值,涉及导数的计算,关键是求出函数f(x)的对称中心.

练习册系列答案
相关题目
19.甘肃省瓜州县自古就以生产“美瓜”面名扬中外,生产的“瓜州蜜瓜”有4个系列30多个品种,质脆汁多,香甜可口,清爽宜人,含糖量达14%~19%,是消暑止渴的佳品,调查表明,蜜瓜的甜度与海拔高度,日照时长,温差有极强的相关性,分别用x,y,z表示蜜瓜甜度与海拔高度,日照时长,温差的相关程度,big对它们进行量化:0表示一般,1表示良,2表示优,在用综合指标w=x+y+z的值平定蜜瓜的顶级,若w≥4,则为一级;若2≤w≤3,则为二级;若0≤w≤1,则为三级,今年来,周边各省也开始发展蜜瓜种植,为了了解目前蜜瓜在周边各省的种植情况,研究人员从不同省份随机抽取了10块蜜瓜种植地,得到如下结果:
(1)若有蜜瓜种植地110块,试估计等级为三家的蜜瓜种植地的数量;
(2)从样本里等级为一级的蜜瓜种植地中随机抽取两块,求这两块种植地的综合指标w至少有一个为4的概率.
| 种植地编号 | A | B | C | D | E |
| (x,y,z) | (1,0,0) | (2,2,1) | (0,1,1) | (2,0,2) | (1,1,1) |
| 种植地编号 | F | G | H | I | J |
| (x,y,z) | (1,1,2) | (2,2,2) | (0,0,1) | (2,2,1) | (0,2,1) |
(2)从样本里等级为一级的蜜瓜种植地中随机抽取两块,求这两块种植地的综合指标w至少有一个为4的概率.
4.已知x,y∈R,( )
| A. | 若|x-y2|+|x2+y|≤1,则${(x+\frac{1}{2})^2}+{(y-\frac{1}{2})^2}≤\frac{3}{2}$ | |
| B. | 若|x-y2|+|x2-y|≤1,则${(x-\frac{1}{2})^2}+{(y-\frac{1}{2})^2}≤\frac{3}{2}$ | |
| C. | 若|x+y2|+|x2-y|≤1,则${(x+\frac{1}{2})^2}+{(y+\frac{1}{2})^2}≤\frac{3}{2}$ | |
| D. | 若|x+y2|+|x2+y|≤1,则${(x-\frac{1}{2})^2}+{(y+\frac{1}{2})^2}≤\frac{3}{2}$ |
8.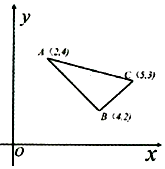 已知点(x,y)在△ABC所包围的阴影区域内(包括边界),若有且仅有B(4,2)是使得z=ax-y取得最大值的最优解,则实数a的取值范围为( )
已知点(x,y)在△ABC所包围的阴影区域内(包括边界),若有且仅有B(4,2)是使得z=ax-y取得最大值的最优解,则实数a的取值范围为( )
 已知点(x,y)在△ABC所包围的阴影区域内(包括边界),若有且仅有B(4,2)是使得z=ax-y取得最大值的最优解,则实数a的取值范围为( )
已知点(x,y)在△ABC所包围的阴影区域内(包括边界),若有且仅有B(4,2)是使得z=ax-y取得最大值的最优解,则实数a的取值范围为( )| A. | -1<a<1 | B. | -1≤a≤1 | C. | -1≤a<1 | D. | -1<a≤1 |