题目内容
5.给甲、乙、丙三人打电话,若打电话的顺序是任意的,则第一个打电话给丙的概率是( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
分析 若打电话的顺序是任意的,则基本事件总数n=3,由此能求出第一个打电话给丙的概率.
解答 解:给甲、乙、丙三人打电话,
若打电话的顺序是任意的,则基本事件总数n=3,
∴第一个打电话给丙的概率是p=$\frac{1}{3}$.
故选:B.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
相关题目
16.若双曲线的右顶点与抛物线y2=12x的焦点相同,它们的离心率之和是3,该双曲线的标准方程是( )
| A. | $\frac{{x}^{2}}{9}-\frac{{y}^{2}}{27}=1$ | B. | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{9}$=1 | C. | $\frac{{x}^{2}}{10}$-$\frac{{y}^{2}}{9}$=1 | D. | $\frac{{x}^{2}}{6}$-$\frac{{y}^{2}}{9}$=1 |
20.为了解适龄公务员对开放生育二胎政策的态度,某部门随机调查了90位三十岁到四十岁的公务员,得到如下列联表,因不慎丢失部分数据.
(1))完成表格数据,判断是否有99%以上的把握认为“生二胎意愿与性别有关”并说明理由;
(2)现从有意愿生二胎的45人中随机抽取2人,求男性公务员和女性公务员各一人的概率.
附:k2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$.
(1))完成表格数据,判断是否有99%以上的把握认为“生二胎意愿与性别有关”并说明理由;
(2)现从有意愿生二胎的45人中随机抽取2人,求男性公务员和女性公务员各一人的概率.
| 男性公务员 | 女性公务员 | 总计 | |
| 有意愿生二胎 | 30 | 15 | 45 |
| 无意愿生二胎 | 20 | 25 | 45 |
| 总计 | 50 | 40 | 90 |
| P(k2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
15.已知集合A={x|22x+1≥4},B={x|y=log2(2-x)},则A∩B=( )
| A. | $\left\{{x\left|{x≥\frac{1}{2}}\right.}\right\}$ | B. | {x|x<2} | C. | $\left\{{x\left|{x≤\frac{1}{2}或x>2}\right.}\right\}$ | D. | $\left\{{x\left|{\frac{1}{2}≤x<2}\right.}\right\}$ |
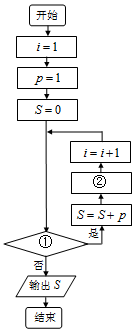 给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推.要求计算这50个数的和.
给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推.要求计算这50个数的和.