题目内容
9.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{a}(2-x),x≤1}\\{|x-5|-1,3≤x≤7}\end{array}\right.$(a>0,且a≠1)的图象上关于直线x=1对称的点有且仅有一对,则实数a的取值范围是( )| A. | [$\frac{1}{7}$,$\frac{1}{5}$]∪{3} | B. | [3,5]∪{$\frac{1}{7}$} | C. | [$\frac{1}{7}$,$\frac{1}{3}$)∪{5} | D. | [3,7)∪{$\frac{1}{5}$} |
分析 若函数f(x)=$\left\{\begin{array}{l}{lo{g}_{a}(2-x),x≤1}\\{|x-5|-1,3≤x≤7}\end{array}\right.$(a>0且a≠1)的图象上关于直线x=1对称的点有且仅有一对,则函数y=logax,与y=|x-5|-1上有且只有一个交点,解得实数a的取值范围.
解答  解:∵函数f(x)=$\left\{\begin{array}{l}{lo{g}_{a}(2-x),x≤1}\\{|x-5|-1,3≤x≤7}\end{array}\right.$(a>0且a≠1)的图象上关于直线x=1对称的点有且仅有一对,
解:∵函数f(x)=$\left\{\begin{array}{l}{lo{g}_{a}(2-x),x≤1}\\{|x-5|-1,3≤x≤7}\end{array}\right.$(a>0且a≠1)的图象上关于直线x=1对称的点有且仅有一对,
∴函数y=logax,与y=|x-5|-1上有且只有一个交点,
当对数函数的图象过(5,-1)点时,a=$\frac{1}{5}$,
当对数函数的图象过(3,1)点时,a=3,
当对数函数的图象过(7,1)点时,a=7,
故a[3,7)∪{$\frac{1}{5}$},
故选:D.
点评 本题考查的知识点是分段函数的应用,注意运用转化思想,转化为函数的图象的交点问题,考查数形结合思想,难度中档.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.过点M($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$)作圆x2+y2=1的切线l,l与x轴的交点为抛物线E:y2=2px(p>0)的焦点,l与抛物线E交于A、B两点,则AB中点到抛物线E的准线的距离为( )
| A. | $\frac{5\sqrt{2}}{2}$ | B. | 3$\sqrt{2}$ | C. | $\frac{7}{2}$$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
17.已知集合A={x|y=$\sqrt{2x-{x}^{2}}$},B={y|y=2x,x∈A},则A∩B=( )
| A. | [0,1) | B. | [1,2] | C. | (2,4] | D. | [2.4] |
14.设a∈R,若复数z=$\frac{a-i}{3+i}$(i是虚数单位)的实部为2,则a的值为( )
| A. | 7 | B. | -7 | C. | 5 | D. | -5 |
1.将数字1,1,2,2,3,3排成三行两列,要求每行的数字互不相同,每列的数字也互不相同,则不同的排列方法共有( )
| A. | 12种 | B. | 18种 | C. | 24种 | D. | 36种 |
 在某次摸底考试中,随机抽取100个人的成绩频率分布直方图如图,若参加考试的共有4000人,那么分数在90分以上的人数约为2600人,根据频率分布直方图估计此次考试成绩的中位数为97.5.
在某次摸底考试中,随机抽取100个人的成绩频率分布直方图如图,若参加考试的共有4000人,那么分数在90分以上的人数约为2600人,根据频率分布直方图估计此次考试成绩的中位数为97.5.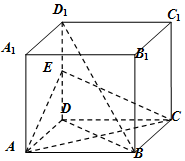 如图,在边长为2的正方体ABCD-A1B1C1D1中,E为DD1中点,
如图,在边长为2的正方体ABCD-A1B1C1D1中,E为DD1中点,