题目内容
1.已知三角形ABC三边分别是a,b,c.边AB上的高为CD,若CD=$\frac{1}{2}$c,则$\frac{2ab}{{(a+b)}^{2}}$的取值范围是[$\sqrt{2}$-1,$\frac{1}{2}$].分析 根据题意,由正弦定理可得c2=2absinC,结合余弦定理可得2absinC=a2+b2-2absinC,变形可得2ab(sinC+cosC)=a2+b2≥2ab,由三角函数恒等变形可得1≤sinC+cosC≤$\sqrt{2}$;则可得$\frac{2ab}{(a+b)^{2}}$=$\frac{1}{sinC+cosC+1}$,结合sinC+cosC的范围,可得$\frac{1}{sinC+cosC+1}$的范围,即可得答案.
解答 解:根据题意,S△ABC=$\frac{1}{2}$absinC=$\frac{1}{2}$•$\frac{1}{2}$•c•c=$\frac{1}{4}$c2,变形可得c2=2absinC,
而c2=a2+b2-2absinC,
则有2absinC=a2+b2-2absinC,变形可得2ab(sinC+cosC)=a2+b2≥2ab,
即sinC+cosC≥1;
而sinC+cosC=$\sqrt{2}$sin(C+$\frac{π}{4}$)≤$\sqrt{2}$,即1≤sinC+cosC≤$\sqrt{2}$;
$\frac{2ab}{(a+b)^{2}}$=$\frac{2ab}{{a}^{2}+{b}^{2}+2ab}$=$\frac{2ab}{2ab(sinC+cosC)+2ab}$=$\frac{1}{sinC+cosC+1}$,
而1≤sinC+cosC≤$\sqrt{2}$,
2≤sinC+cosC+1≤$\sqrt{2}$+1,
$\sqrt{2}$-1≤$\frac{1}{sinC+cosC+1}$≤$\frac{1}{2}$,
即$\sqrt{2}$-1≤$\frac{2ab}{{(a+b)}^{2}}$≤$\frac{1}{2}$,
故答案为:[$\sqrt{2}$-1,$\frac{1}{2}$]
点评 本题考查三角函数的最值,关键是利用正弦、余弦定理进行化简、变形,找到$\frac{2ab}{{(a+b)}^{2}}$与sinC+cosC的关系.

| A. | 平行 | B. | 相交 | C. | 异面 | D. | 垂直 |
| 观看场数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 观看人数占调查人数的百分比 | 8% | 10% | 20% | 26% | 16% | m% | 6% | 2% |
| A. | 表中m的数值为8 | |
| B. | 估计观看比赛不低于4场的学生约为360人 | |
| C. | 估计观看比赛不低于4场的学生约为720人 | |
| D. | 若从1000名学生中抽取样容量为50的学生时采用系统抽样,则分段的间隔为25 |
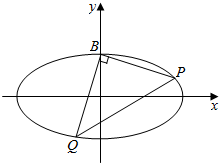 如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率是$\frac{{\sqrt{3}}}{2}$,一个顶点是B(0,1).
如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率是$\frac{{\sqrt{3}}}{2}$,一个顶点是B(0,1).