题目内容
7.已知抛物线y2=4x与双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)有相同的焦点F,点A是两曲线的一个交点,点B是点F关于坐标原点的对称点,且以AB为直径的圆过点F,则双曲线的离心率为( )| A. | 2$\sqrt{2}$-1 | B. | $\sqrt{2}$+1 | C. | 8$\sqrt{2}$-8 | D. | 2$\sqrt{2}$-2 |
分析 由题意可知:B点坐标(-1,0),AF⊥BF,则|AF|=2,A(1,2),代入椭圆方程,即可求得a的值,求得椭圆的离心率.
解答  解:由题意可知:双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)焦点坐标为(1,0),(-1,0),c=1,
解:由题意可知:双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)焦点坐标为(1,0),(-1,0),c=1,
由点B是点F关于坐标原点的对称点,则B(-1,0),
以AB为直径的圆过点F,
则AF⊥BF,
设A点在第一象限,
∴|AF|=2,
∴A(1,2),
∵点A在双曲线上,
∴$\frac{1}{{a}^{2}}-\frac{4}{{b}^{2}}=1$,
∵c=1,b2=c2-a2,
∴a=$\sqrt{2}$-1,
∴e=$\frac{c}{a}$=$\sqrt{2}$+1,
故选B.
点评 本题考查双曲线的简单几何性质,考查双曲线的离心率,考查计算能力,属于中档题.

练习册系列答案
相关题目
18.某校为了解学生学习的情况,采用分层抽样的方法从高一1000人、高二1200人、高三n人中,抽取81人进行问卷调查.已知高二被抽取的人数为30,那么n=( )
| A. | 860 | B. | 720 | C. | 1020 | D. | 1040 |
18.下列函数中,既是偶函数,又在区间(1,2)上是减函数的为( )
| A. | y=log${\;}_{\frac{1}{2}}$|x| | B. | y=x${\;}^{\frac{1}{2}}$ | C. | y=$\frac{{{2^x}+{2^{-x}}}}{2}$ | D. | y=lg$\frac{2-x}{2+x}$ |
2.已知三个数a=0.60.3,b=log0.63,c=lnπ,则a,b,c的大小关系是( )
| A. | c<b<a | B. | c<a<b | C. | b<c<a | D. | b<a<c |
 ,若
,若 ,则
,则 ( )
( )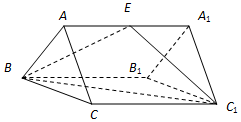 如图:三棱柱ABC-A1B1C1的所有棱长均相等,AA1⊥平面ABC,E为AA1的中点.
如图:三棱柱ABC-A1B1C1的所有棱长均相等,AA1⊥平面ABC,E为AA1的中点. ,则
,则 ________
________  __________.
__________.