题目内容

2．已知三个数a=0.60.3，b=log0.63，c=lnπ，则a，b，c的大小关系是（　　）
A．c＜b＜aB．c＜a＜bC．b＜c＜aD．b＜a＜c

分析 利用指数函数与对数函数的单调性即可得出．

解答 解：三个数a=0.60.3∈（0，1），b=log0.63＜0，c=lnπ＞1，
∴c＞a＞b．
故选：D．

点评 本题考查了指数函数与对数函数的单调性，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
13．若${（{x-\frac{a}{x^2}}）^9}$的二项展开式中含x6项的系数为36，则实数a=-4．
13．已知正四棱锥的底面边长为4cm，高与侧棱夹角为45°，则其斜高长为$2\sqrt{3}$（cm）．
10．下列结论中错误的是（　　）
A．若0＜α＜$\frac{π}{2}$，则sinα＜tanα
B．若α是第二象限角，则$\frac{α}{2}$为第一象限或第三象限角
C．若角α的终边过点P（3k，4k）（k≠0），则sinα=$\frac{4}{5}$
D．若扇形的周长为6，半径为2，则其中心角的大小为1弧度
17．甲、乙、丙三人组成一个小组参加电视台主办的听曲猜哥歌名活动，在每一轮活动中，依次播放三首乐曲，然后甲猜第一首，乙猜第二首，丙猜第三首．若有一人猜错，则活动立即结束；若三人均猜对，则该小组进入下一轮．该小组最多参加三轮活动．已知每一轮甲猜对歌名的概率是$\frac{3}{4}$，乙猜对歌名的概率是$\frac{2}{3}$，丙猜对歌名的概率是$\frac{1}{2}$．甲、乙、丙猜对互不影响．
（1）求该小组未能进入第二轮的概率；
（2）记乙猜歌曲的次数为随机变量ξ，求ξ的分布列和数学期望．
7．已知抛物线y2=4x与双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）有相同的焦点F，点A是两曲线的一个交点，点B是点F关于坐标原点的对称点，且以AB为直径的圆过点F，则双曲线的离心率为（　　）
A．2$\sqrt{2}$-1B．$\sqrt{2}$+1C．8$\sqrt{2}$-8D．2$\sqrt{2}$-2
13．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$满足：|$\overrightarrow{a}$|=2，|$\overrightarrow{b}$|=4，＜$\overrightarrow{a}$，$\overrightarrow{b}$＞=$\frac{π}{3}$，则|3$\overrightarrow{a}$-2$\overrightarrow{b}$|=（　　）
A．52B．$2\sqrt{13}$C．100-48$\sqrt{3}$D．$\sqrt{100-48\sqrt{3}}$
9．一个几何体的三视图如图所示（单位：cm），则此几何体的表面积是（　　）
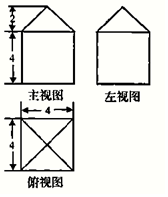
A．96+16$\sqrt{2}$cm2B．80+16$\sqrt{2}$cm2C．96+32$\sqrt{2}$cm2D．80+32$\sqrt{2}$cm2

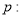已知命题指数函数在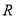上是单调函数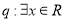；命题，.若命题“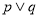”为真命题，命题“”为假命题，求实数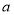的取值范围.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网