题目内容
7.已知函数f(x)=(1-k)x+$\frac{m}{x}$+2,其中k,m∈R,且m≠0.(1)求函数f(x)的定义域;
(2)k如何取值时,方程f(x)=0有解,并求出方程的解.
分析 (1)由题意得,x≠0,从而写出定义域即可;
(2)分类讨论首先确定函数是对勾函数还是反比例函数,当是对勾函数时再讨论即可.
解答 解:(1)由题意得,x≠0,
故函数f(x)的定义域为{x|x≠0};
(2)(i)当1-k=0,即k=1时,方程f(x)=0的解为x=-$\frac{2}{m}$;
(ii)当k≠1时,方程f(x)=0可化为
$\frac{(1-k){x}^{2}+2x+m}{x}$=0,
∵m≠0,
∴原方程可化为(1-k)x2+2x+m=0,
∴①当△=4-4(1-k)m<0,即(1-k)m>1时,
方程f(x)=0无解,
②当△=4-4(1-k)m=0,即(1-k)m=1时,
方程f(x)=0有且只有一个解x=-$\frac{1}{1-k}$=$\frac{1}{k-1}$;
③当△=4-4(1-k)m>0,即(1-k)m<1时,
方程f(x)=0有两个解,x=$\frac{1±\sqrt{1-(1-k)m}}{k-1}$.
点评 本题考查了函数的定义域的求法及分类讨论的思想应用.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
17.在复平面内,复数z和$\frac{1+i}{1-2i}$所表示的点关于虚轴对称,则z=( )
| A. | -$\frac{1}{5}$+$\frac{3}{5}$i | B. | $\frac{1}{5}$+$\frac{3}{5}$i | C. | $\frac{1}{5}$-$\frac{3}{5}$i | D. | -$\frac{1}{5}$-$\frac{3}{5}$i |
2.已知函数f(2x+1)=4x2+4x-5,则f(3)=( )
| A. | 43 | B. | -3 | C. | 2 | D. | 3 |
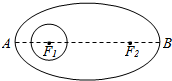 1998年12月19日,太原卫星发射中心为摩托罗拉公司(美国)发射了“铱星”系统通信卫星,卫星运行的轨道是椭圆,F1、F2是其焦点,地球中心为焦点F1,设地球半径为m,已知椭圆轨道的近地点A(离地面最近的点)距地面$\frac{m}{3}$,远地点B(离地面最远的点)距地面3m,并且F1、A、B在同一直线上,求卫星运行的轨道方程.
1998年12月19日,太原卫星发射中心为摩托罗拉公司(美国)发射了“铱星”系统通信卫星,卫星运行的轨道是椭圆,F1、F2是其焦点,地球中心为焦点F1,设地球半径为m,已知椭圆轨道的近地点A(离地面最近的点)距地面$\frac{m}{3}$,远地点B(离地面最远的点)距地面3m,并且F1、A、B在同一直线上,求卫星运行的轨道方程.