题目内容
12.已知f(x)=m(x-2m)(x+m+1),g(x)=2x-1,若?x∈R,f(x)<0或g(x)<0,则实数m的取值范围为(-1,0).分析 根据题意得出f(x)=m(x-2m)(x+m+3)<0在x≥0时恒成立,建立关于m的不等式组,从而求出m的取值范围.
解答 解:∵g(x)=2x-1,且当x≥0时,g(x)≥0,
又?x∈R时,f(x)<0或g(x)<0,
∴f(x)=m(x-2m)(x+m+1)<0在x≥0时恒成立,
∴二次函数f(x)的图象开口只能向下,且与x轴交点都在原点(0,0)的左侧,
即$\left\{\begin{array}{l}{m<0}\\{2m<0}\\{-m-1<0}\end{array}\right.$,
解得-1<m<0;
∴m的取值范围是(-1,0).
点评 本题考查了二次函数和指数函数的综合应用问题,也考查了全称命题的应用问题,是基础题目.

练习册系列答案
相关题目
4.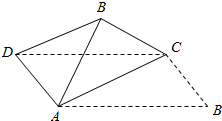 如图,将矩形纸片ABCD(其中$AB=\sqrt{3}$,BC=1)沿对角线AC折起后,使得异面直线BC⊥AD,则此时异面直线AB和CD所成的角的余弦值是( )
如图,将矩形纸片ABCD(其中$AB=\sqrt{3}$,BC=1)沿对角线AC折起后,使得异面直线BC⊥AD,则此时异面直线AB和CD所成的角的余弦值是( )
 如图,将矩形纸片ABCD(其中$AB=\sqrt{3}$,BC=1)沿对角线AC折起后,使得异面直线BC⊥AD,则此时异面直线AB和CD所成的角的余弦值是( )
如图,将矩形纸片ABCD(其中$AB=\sqrt{3}$,BC=1)沿对角线AC折起后,使得异面直线BC⊥AD,则此时异面直线AB和CD所成的角的余弦值是( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
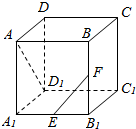 长方体ABCD-A1B1C1D1中,AB=BC=2a,AA1=a,E和F分别是A1B1和BB1的中点,求:
长方体ABCD-A1B1C1D1中,AB=BC=2a,AA1=a,E和F分别是A1B1和BB1的中点,求: