题目内容
17.在复平面内,复数z和$\frac{1+i}{1-2i}$所表示的点关于虚轴对称,则z=( )| A. | -$\frac{1}{5}$+$\frac{3}{5}$i | B. | $\frac{1}{5}$+$\frac{3}{5}$i | C. | $\frac{1}{5}$-$\frac{3}{5}$i | D. | -$\frac{1}{5}$-$\frac{3}{5}$i |
分析 由复数代数形式的乘除运算化简$\frac{1+i}{1-2i}$,又复数z和$\frac{1+i}{1-2i}$所表示的点关于虚轴对称,则答案可求.
解答 解:∵$\frac{1+i}{1-2i}$=$\frac{(1+i)(1+2i)}{(1-2i)(1+2i)}=\frac{-1+3i}{5}=-\frac{1}{5}+\frac{3}{5}i$,
又复数z和$\frac{1+i}{1-2i}$所表示的点关于虚轴对称,
∴z=$\frac{1}{5}+\frac{3}{5}i$.
故选:B.
点评 本题考查了复数代数形式的乘除运算,考查了复数的代数表示法及其几何意义,是基础题.

练习册系列答案
相关题目
8.下列函数是奇函数的是( )
| A. | f(x)=(x-1)$\sqrt{\frac{1+x}{1-x}}$ | B. | f(x)=$\frac{|x|}{x}$ | ||
| C. | f(x)=$\left\{\begin{array}{l}{1+x,(x≥0)}\\{1-x(x<0)}\end{array}\right.$ | D. | f(x)=$\frac{1}{x-1}$ |
5.已知向量$\overrightarrow a$,$\overrightarrow b$满足$|{\overrightarrow a}|=2$,$|{\overrightarrow b}|=1$且$({\overrightarrow a+\overrightarrow b})⊥\overrightarrow b$,则$\overrightarrow a$与$\overrightarrow b$的夹角为( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{6}$ |
12.从(40,30),(50,10),(20,30),(45,5),(10,10)这5个点中任取一个点,这个点在圆x2+y2=2016内部的概率是( )
| A. | $\frac{3}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{4}{5}$ |
9.当-1≤x≤1,函数y=2x-2的值域为( )
| A. | [-$\frac{3}{2}$,0] | B. | [0,$\frac{3}{2}$] | C. | [-1,0] | D. | [-$\frac{3}{2}$,1] |
6.小军旅行箱的密码是一个六位数,由于他忘记了密码的末位数字,则小军能一次打开该旅行箱的概率是( )
| A. | $\frac{1}{10}$ | B. | $\frac{1}{9}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{5}$ |
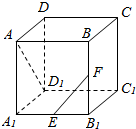 长方体ABCD-A1B1C1D1中,AB=BC=2a,AA1=a,E和F分别是A1B1和BB1的中点,求:
长方体ABCD-A1B1C1D1中,AB=BC=2a,AA1=a,E和F分别是A1B1和BB1的中点,求: