题目内容
2.已知函数$f(x)={log_3}(\frac{1}{x}+a)(a>0)$,对任意的$t∈[\frac{1}{4},1]$,函数f(x)在区间[t,t+1]上的最大值与最小值的差不超过1,则a的取值范围为[$\frac{4}{5}$,+∞).分析 由对数的性质,结合复合函数的性质可得f(t)取得最大值,f(t+1)取得最小值.根据对数运算转化为二次函数在$t∈[\frac{1}{4},1]$恒成立问题,即可求出a的范围.
解答 解:函数$f(x)={log_3}(\frac{1}{x}+a)(a>0)$,令u=$\frac{1}{x}+a$,
由对数函数的性质可知,f(u)=log3u在定义域内单调递增.
函数u=$\frac{1}{x}+a$,在[t,t+1]上单调递减.
根据复合函数的性质,可得f(t)取得最大值,f(t+1)取得最小值.
∴f(t)-f(t+1)≤1,即$lo{g}_{3}(\frac{1}{t}+a)-lo{g}_{3}(\frac{1}{t+1}+a)≤1$对任意的$t∈[\frac{1}{4},1]$恒成立.
可得:2at2+(2a+2)t-1≥0对任意的$t∈[\frac{1}{4},1]$恒成立.
其对称轴t=-$\frac{a+2}{2}$=$-1-\frac{a}{2}$,a>0,
∴二次函数在$t∈[\frac{1}{4},1]$单调递增,
当t=$\frac{1}{4}$时,可得最小值为2a×$\frac{1}{16}$+(2a+2)×$\frac{1}{4}$-1≥0.
解得:a≥$\frac{4}{5}$.
则a的取值范围为[$\frac{4}{5}$,+∞).
故答案为:[$\frac{4}{5}$,+∞).
点评 本题考查了考查了对数的性质,结合复合函数的性质,以及二次函数在$t∈[\frac{1}{4},1]$恒成立问题讨论问题,属于中档题.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
17.某几何体的三视图如图所示(网格中的小正方形边长为),则该几何体的体积为( )


| A. | $\frac{16}{3}$ | B. | $\frac{10}{3}$ | C. | $\frac{8}{3}$ |
7.化简$C_n^0-2C_n^1+{2^2}C_n^2+…+{(-1)^n}{2^n}C_n^n$=( )
| A. | 1 | B. | -1 | C. | (-1)n | D. | (-1)n-1 |
14.已知某几何体的三视图如图所示,则该几何体的体积为( )
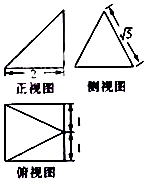

| A. | $\frac{4}{3}$$\sqrt{5}$ | B. | 4$\sqrt{5}$ | C. | $\frac{8}{3}$ | D. | 8 |
11.正整数按如表的规律排列,则第2017行,第2016列的数应为( )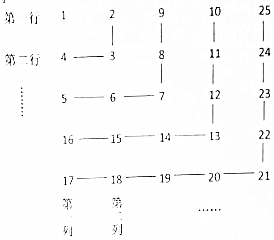

| A. | 20162 | B. | 2016×2017 | C. | 20172 | D. | 2017×2018 |
12.如图,第n个图形是由正n+2边形“扩展”而来,(n=1、2、3、…),则在第5个图形中共有( )个顶点.


| A. | 48 | B. | 52 | C. | 56 | D. | 60 |
