题目内容
已知椭圆方程为
+
=1(a>b>0),F1、F2分别为其上、下两个焦点,F1(0,1),F2(0,-1),过F2斜率为1的直线与椭圆交于A、B两点,且|AB|=
.
(1)求椭圆的方程;
(2)C、D为椭圆的上、下顶点,是否存在直线y=m,使得该直线上的任意点P(x0,m)满足PC、PD与椭圆的另一交点M、N,MN的连线恒过F2.
| y2 |
| a2 |
| x2 |
| b2 |
| 24 |
| 7 |
(1)求椭圆的方程;
(2)C、D为椭圆的上、下顶点,是否存在直线y=m,使得该直线上的任意点P(x0,m)满足PC、PD与椭圆的另一交点M、N,MN的连线恒过F2.
考点:椭圆的应用,椭圆的简单性质
专题:计算题,作图题,圆锥曲线的定义、性质与方程
分析:(1)由题意做出图象,借助图象可知,a2=b2+1,将直线方程与椭圆方程联立,利用根与系数的关系及两点间的距离公式可得,(x1-x2)2=(
)2-4
=(
•
)2,从而可得
=
,进而求出椭圆的方程.
(2)假设存在,设出直线方程,与椭圆方程联立,解出点M的坐标为(-
,-
+2),点N的坐标为(
,
-2),由M、N、F2,三点共线可知斜率相等,从而得到-
•(
-2+1)-
•(-
+2+1)=0对任意x0都成立,从而解出m.
| 2b2 |
| 2b2+1 |
| -b4 |
| 2b2+1 |
| 24 |
| 7 |
| ||
| 2 |
| 8b4(b2+1) |
| (2b2+1)2 |
| 288 |
| 49 |
(2)假设存在,设出直线方程,与椭圆方程联立,解出点M的坐标为(-
| 12(m-2)x0 | ||
3(m-2)2+4
|
| 12(m-2)2 | ||
3(m-2)2+4
|
| 12(m+2)x0 | ||
3(m+2)2+4
|
| 12(m+2)2 |
| 3(m+2)2+4x02 |
| 12(m-2)x0 | ||
3(m-2)2+4
|
| 12(m+2)2 |
| 3(m+2)2+4x02 |
| 12(m+2)x0 | ||
3(m+2)2+4
|
| 12(m-2)2 | ||
3(m-2)2+4
|
解答:
解: (1)如右图:由题意知,c=1,则a2=b2+1,
(1)如右图:由题意知,c=1,则a2=b2+1,
过F2斜率为1的直线方程为y=x-1,与椭圆方程
+
=1联立消y可得,
+
=1,即(2b2+1)x2-2b2x-b4=0,
设A、B两点的横坐标分别为x1,x2,则
x1+x2=
,x1x2=
,又∵|AB|=
,
则(x1-x2)2=(
)2-4
=(
•
)2,
即
=
,
解得,b2=3,则a2=b2+1=4;
则椭圆的方程为
+
=1.
(2)假设存在直线y=m,使得该直线上的任意点P(x0,m)满足PC、PD与椭圆的另一交点M、N,MN的连线恒过F2.
C(0,2),D(0,-2),
则直线CP的方程为y=
x+2,与
+
=1联立消去y化简可得.
(3(
)2+4)x2+12
x=0,
解得,x=0或x=-
;
则点M的坐标为(-
,-
+2),
同理,点N的坐标为(
,
-2),
则由M、N、F2,三点共线可知,
-
•(
-2+1)-
•(-
+2+1)=0,
即:
•(
-1)-
•(
-3)=0,
即x0[9(m+2)2(m-2)-3(m-2)2(m+2)-4x02[(m-2)-3(m+2)]]=0,
∵x0任意,则9(m+2)2(m-2)-3(m-2)2(m+2)=0且(m-2)-3(m+2)=0,
解得,m=-4.
 (1)如右图:由题意知,c=1,则a2=b2+1,
(1)如右图:由题意知,c=1,则a2=b2+1,过F2斜率为1的直线方程为y=x-1,与椭圆方程
| y2 |
| a2 |
| x2 |
| b2 |
| (x-1)2 |
| b2+1 |
| x2 |
| b2 |
设A、B两点的横坐标分别为x1,x2,则
x1+x2=
| 2b2 |
| 2b2+1 |
| -b4 |
| 2b2+1 |
| 24 |
| 7 |
则(x1-x2)2=(
| 2b2 |
| 2b2+1 |
| -b4 |
| 2b2+1 |
| 24 |
| 7 |
| ||
| 2 |
即
| 8b4(b2+1) |
| (2b2+1)2 |
| 288 |
| 49 |
解得,b2=3,则a2=b2+1=4;
则椭圆的方程为
| y2 |
| 4 |
| x2 |
| 3 |
(2)假设存在直线y=m,使得该直线上的任意点P(x0,m)满足PC、PD与椭圆的另一交点M、N,MN的连线恒过F2.
C(0,2),D(0,-2),
则直线CP的方程为y=
| m-2 |
| x0 |
| y2 |
| 4 |
| x2 |
| 3 |
(3(
| m-2 |
| x0 |
| m-2 |
| x0 |
解得,x=0或x=-
| 12(m-2)x0 | ||
3(m-2)2+4
|
则点M的坐标为(-
| 12(m-2)x0 | ||
3(m-2)2+4
|
| 12(m-2)2 | ||
3(m-2)2+4
|
同理,点N的坐标为(
| 12(m+2)x0 | ||
3(m+2)2+4
|
| 12(m+2)2 |
| 3(m+2)2+4x02 |
则由M、N、F2,三点共线可知,
-
| 12(m-2)x0 | ||
3(m-2)2+4
|
| 12(m+2)2 |
| 3(m+2)2+4x02 |
| 12(m+2)x0 | ||
3(m+2)2+4
|
| 12(m-2)2 | ||
3(m-2)2+4
|
即:
| 12(m-2)x0 | ||
3(m-2)2+4
|
| 12(m+2)2 |
| 3(m+2)2+4x02 |
| 12(m+2)x0 | ||
3(m+2)2+4
|
| 12(m-2)2 | ||
3(m-2)2+4
|
即x0[9(m+2)2(m-2)-3(m-2)2(m+2)-4x02[(m-2)-3(m+2)]]=0,
∵x0任意,则9(m+2)2(m-2)-3(m-2)2(m+2)=0且(m-2)-3(m+2)=0,
解得,m=-4.
点评:本题考查了椭圆的方程的求法解三点共线问题,同时考查了圆锥曲线与直线的交点问题及恒成立问题,属于难题.

练习册系列答案
相关题目
若f′(x0)=-3,则
=( )
| lim |
| h→0 |
| f(x0+h)-f(x0-h) |
| h |
| A、-3 | B、-6 | C、-9 | D、-12 |
在公比为整数的等比数列{an}中,若,a1+a3=6,a2+a4=12,则a3等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
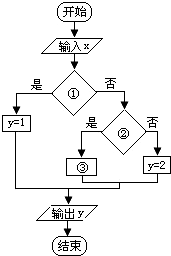 任给x的值,计算函数y=
任给x的值,计算函数y=
|
| A、x<1、x>1、y=3 |
| B、x=1、x>1、y=3 |
| C、x<1、x=1、y=3 |
| D、x<1、x>1、y=3 |
已知△ABC中,sinA:sinB:sinC=1:1:
,则此三角形的最大内角的度数是( )
| 3 |
| A、60° | B、90° |
| C、120° | D、135° |
在等差数列{an}中,已知前三项和为15,最后三项和为78,所有项和为155,则项数n=( )
| A、8 | B、9 | C、10 | D、11 |
函数y=f(x)在R上为减函数,且f(2m)>f(-m+9),则实数m的取值范围是( )
| A、(-∞,3) |
| B、(0,+∞) |
| C、(3,+∞) |
| D、(-∞,-3)∪(3,+∞) |