题目内容
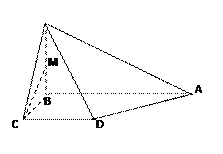
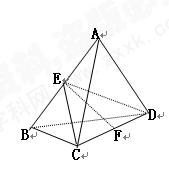
如图,在四棱锥
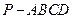 中,
中,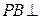 平面
平面 ,
, 底面
底面 是一个直角梯形,
是一个直角梯形,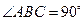 ,
,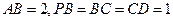 。
。(1) 若
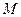 为
为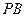 的中点,证明:直线
的中点,证明:直线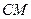 ∥平面
∥平面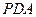 ;
;(2) 求二面角
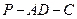 的余弦值。
的余弦值。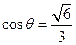
(1)取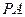 中点
中点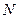 ,连结
,连结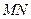 ,
,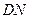 ,可证
,可证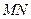 ∥
∥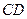 且
且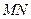 =
=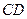 ,∴
,∴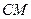 ∥
∥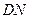 ,
,
又∵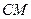
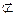 平面
平面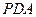 ,
,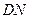
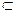 平面
平面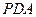
∴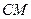 ∥平面
∥平面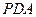
(2)(法一)连结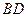 ,在梯形
,在梯形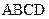 中,
中,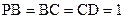 ,
,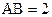
∴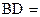
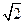 ,又可得
,又可得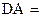
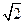 ,
,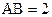 ,∴
,∴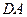 ⊥
⊥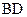 ,
,
∵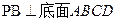 ,
,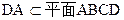 ∴
∴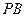 ⊥
⊥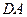 ,
,
又∵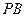
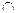
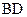
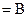 ,
,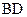 ,
,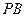

∴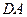 ⊥平面
⊥平面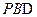 ,
,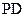

∴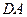 ⊥
⊥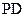
∴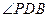 为二面角
为二面角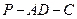 的平面角
的平面角
∴在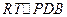 中,
中,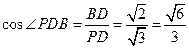
∴二面角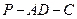 余弦值为
余弦值为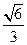 。
。
(法二)以B为原点,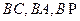 所在直线为
所在直线为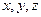 轴建立直角坐标系,则
轴建立直角坐标系,则
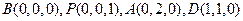
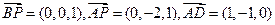
∵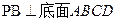
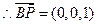 是平面
是平面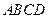 的一个法向量
的一个法向量
设平面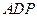 的一个法向量为
的一个法向量为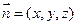 ,则
,则
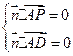 ,即
,即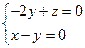
令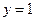 ,则
,则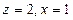 ,∴
,∴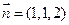
∴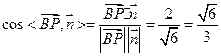
设二面角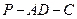
 的平面角为
的平面角为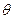 ,则
,则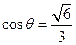
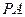 中点
中点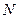 ,连结
,连结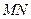 ,
,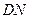 ,可证
,可证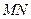 ∥
∥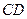 且
且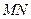 =
=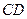 ,∴
,∴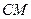 ∥
∥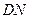 ,
,又∵
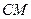
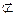 平面
平面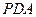 ,
,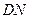
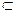 平面
平面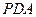
∴
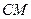 ∥平面
∥平面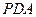
(2)(法一)连结
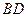 ,在梯形
,在梯形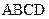 中,
中,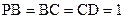 ,
,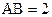
∴
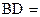
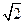 ,又可得
,又可得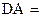
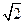 ,
,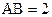 ,∴
,∴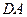 ⊥
⊥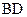 ,
,∵
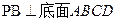 ,
,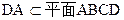 ∴
∴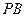 ⊥
⊥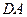 ,
,又∵
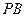
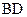
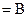 ,
,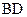 ,
,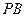

∴
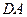 ⊥平面
⊥平面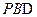 ,
,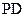

∴
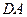 ⊥
⊥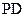
∴
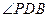 为二面角
为二面角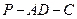 的平面角
的平面角∴在
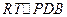 中,
中,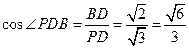
∴二面角
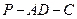 余弦值为
余弦值为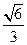 。
。(法二)以B为原点,
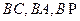 所在直线为
所在直线为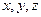 轴建立直角坐标系,则
轴建立直角坐标系,则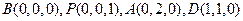
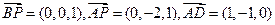
∵
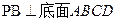
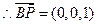 是平面
是平面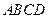 的一个法向量
的一个法向量设平面
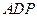 的一个法向量为
的一个法向量为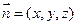 ,则
,则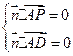 ,即
,即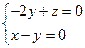
令
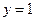 ,则
,则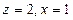 ,∴
,∴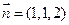
∴
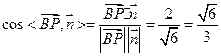
设二面角
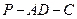
 的平面角为
的平面角为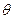 ,则
,则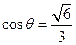

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
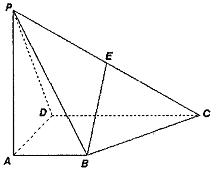
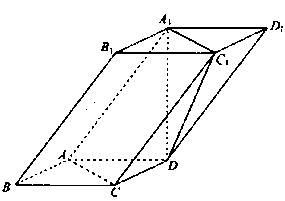
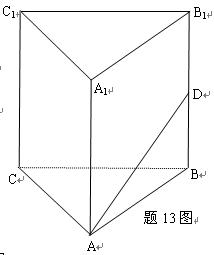
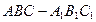 是各棱长为5的正三棱柱,
是各棱长为5的正三棱柱,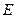 ,
,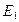 分别是
分别是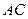 ,
,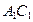 的中点,则平面
的中点,则平面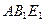 与平面
与平面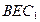 的距离为多少
的距离为多少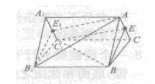
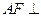 平面PCD;(2)求证:平面PCE⊥平面PCD.
平面PCD;(2)求证:平面PCE⊥平面PCD.
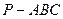 中,
中,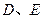 分别是
分别是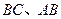 的中点,
的中点,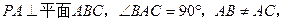
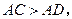
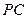 与
与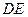 所成的角为
所成的角为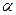 ,
,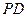 与平面
与平面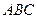 所成的角为
所成的角为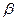 ,二面角
,二面角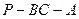 的平面角为
的平面角为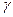 ,则
,则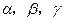 的大小关系是 ( )
的大小关系是 ( ) 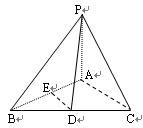
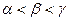
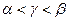
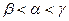
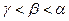
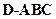 的外接球的球心O满足
的外接球的球心O满足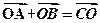 ,且外接球的体积为
,且外接球的体积为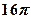 ,则该三棱锥的体积为 .
,则该三棱锥的体积为 . 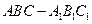 中,已知
中,已知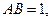 点
点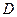 在棱
在棱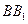 上,且
上,且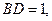 且
且
 与平面
与平面 所成的角的正弦值是_
所成的角的正弦值是_ ___________.
___________.
 是边长为
是边长为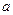 的正三角形
的正三角形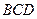 所在平面外一点,
所在平面外一点,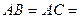
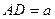 ,
,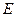 、
、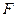 分别是
分别是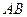 、
、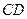 中点,
中点,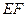 为异面直线
为异面直线