题目内容
(本题满分12分) 如图,四棱锥P—ABCD的底面ABCD为一直角梯形,其中BA⊥AD,CD⊥AD,CD=AD=2AB,PA⊥底面ABCD,E是PC的中点。
(1)求证:BE//平面PAD;
(2)若BE⊥平面PCD,①求异面直线PD与BC所成角的余弦值;
②求二面角E—BD—C的余弦值。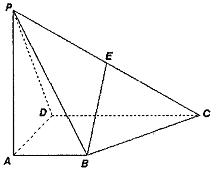
(1)求证:BE//平面PAD;
(2)若BE⊥平面PCD,①求异面直线PD与BC所成角的余弦值;
②求二面角E—BD—C的余弦值。

略
设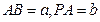 ,建立如图的空间坐标系,
,建立如图的空间坐标系,
 ,
, ,
,
 ,
,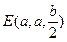 .……………………………………2分
.……………………………………2分
(1) ,
,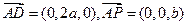 ,
,
所以 ,
,
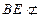 平面
平面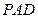 ,
,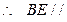 平面
平面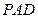 .
.  ……………………………………4分
……………………………………4分
(2) 平面
平面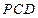 ,
,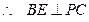 ,即
,即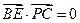
 ,
,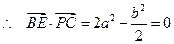 ,即
,即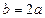 .………
.……… …………6分
…………6分
①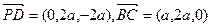 ,
,
 ,
,
所以异面直线 与
与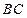 所成角的余弦值为
所成角的余弦值为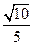 ……………………………8分
……………………………8分
②平面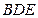 和平面
和平面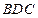 中,
中,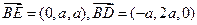
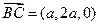 ,
,
所以平面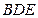 的一个法向量为
的一个法向量为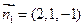 ;……………………………………9分
;……………………………………9分
平面 的一个法向量为
的一个法向量为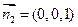 ;……………………………………10分
;……………………………………10分
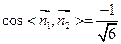 ,所以二面角
,所以二面角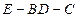 的余弦值为
的余弦值为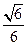 …………………12分
…………………12分
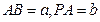 ,建立如图的空间坐标系,
,建立如图的空间坐标系, ,
, ,
, ,
,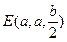 .……………………………………2分
.……………………………………2分(1)
 ,
,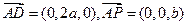 ,
,所以
 ,
, 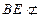 平面
平面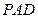 ,
,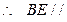 平面
平面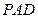 .
.  ……………………………………4分
……………………………………4分(2)
 平面
平面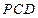 ,
,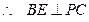 ,即
,即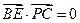
 ,
,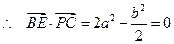 ,即
,即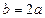 .………
.……… …………6分
…………6分①
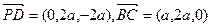 ,
, ,
,所以异面直线
 与
与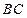 所成角的余弦值为
所成角的余弦值为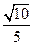 ……………………………8分
……………………………8分②平面
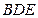 和平面
和平面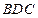 中,
中,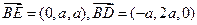
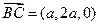 ,
,所以平面
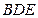 的一个法向量为
的一个法向量为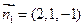 ;……………………………………9分
;……………………………………9分平面
 的一个法向量为
的一个法向量为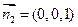 ;……………………………………10分
;……………………………………10分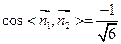 ,所以二面角
,所以二面角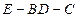 的余弦值为
的余弦值为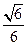 …………………12分
…………………12分
练习册系列答案
相关题目
 F 在 EA 上且 B1F⊥AE,试求点 F 的坐标;
F 在 EA 上且 B1F⊥AE,试求点 F 的坐标;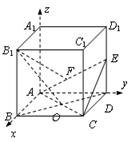
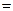 a,AD
a,AD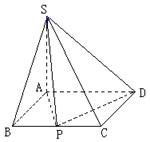
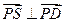 .
. 个单位法向量
个单位法向量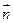
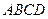 中,
中,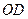 垂直平分
垂直平分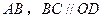 ,且
,且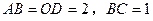 ,现将四边形
,现将四边形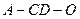 的正弦值;
的正弦值;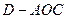 的体积.
的体积.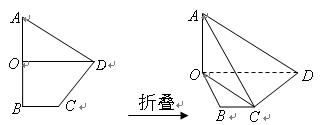
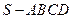 中,底面
中,底面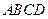 是正方形,其他四个侧面都是等边三角形,
是正方形,其他四个侧面都是等边三角形,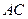 与
与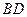 的交点为O.
的交点为O. 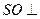 平面
平面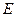 为侧棱
为侧棱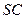 上一个动点. 试问对于
上一个动点. 试问对于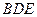 与平面
与平面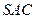 是否垂直?若垂直,请加以证明;若不垂直,请
是否垂直?若垂直,请加以证明;若不垂直,请 说明理由.
说明理由.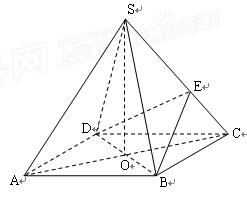
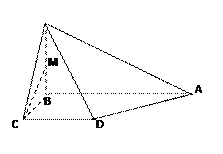
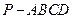 中,
中,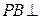 平面
平面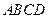 ,
, 底面
底面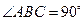 ,
,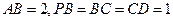 。
。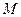 为
为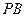 的中点,证明:直线
的中点,证明:直线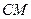 ∥平面
∥平面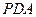 ;
;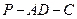 的余弦值。
的余弦值。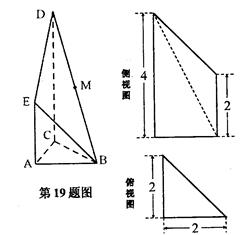
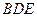 ?若存在,确定点N的位置;
?若存在,确定点N的位置; 若不存在,请说明理由.
若不存在,请说明理由. 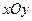 中,已知平面区域
中,已知平面区域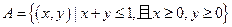 ,则平面区域
,则平面区域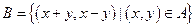 的面积为( )
的面积为( )