题目内容
(本小题满分13分)
如图,已知四棱柱ABCD—A1B1C1D1中,A1D⊥底面ABCD,底面ABCD是边长为1的正方形,侧棱AA1=2。
(I)求证:C1D//平面ABB1A1;
(II)求直线BD1与平面A1C1D所成角的正弦值;
(Ⅲ)求二面角D—A1C1—A的余弦值。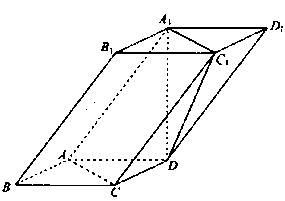
如图,已知四棱柱ABCD—A1B1C1D1中,A1D⊥底面ABCD,底面ABCD是边长为1的正方形,侧棱AA1=2。
(I)求证:C1D//平面ABB1A1;
(II)求直线BD1与平面A1C1D所成角的正弦值;
(Ⅲ)求二面角D—A1C1—A的余弦值。

(1)略(2) (3)
(3)
 (3)
(3)
(I)证明:四棱柱ABCD—A1B1C1D1中,BB1//CC1,
又 面ABB1A1,所以CC1//平面ABB1A1, …………2分
面ABB1A1,所以CC1//平面ABB1A1, …………2分
ABCD是正方形,所以CD//AB,
又CD 面ABB1A1,所以CD//平面ABB1A1, …………3分
面ABB1A1,所以CD//平面ABB1A1, …………3分
所以平面CDD1C1//平面ABB1A1,
所以C1D//平面ABB1A1 …………4分
(II)解:ABCD是正方形,AD⊥CD
因为A1D⊥平面ABCD,
所以A1D⊥AD,A1D⊥CD,
如图,以D为原点建立空间直角坐标系D—xyz, …………5分

在 中,由已知可得
中,由已知可得
所以 ,
,

 …………6分
…………6分
因为A1D⊥平面ABCD,
所以A1D⊥平面A1B1C1D1
A1D⊥B1D1。
又B1D1⊥A1C1,
所以B1D1⊥平面A1C1D, …………7分
所以平面A1C1D的一个法向量为n=(1,1,0 ) …………8分
) …………8分
设 与n所成的角为
与n所成的角为 ,
,
则 …………9分
…………9分
所以直线BD1与平面A1C1D所成角的正弦值为 …………10分
…………10分
(III)解:平面A1C1A的法向量为
则
所以
令 可得
可得 …………12分
…………12分
设二面角D—A1C1—A的大小为a,
则
所以二面角 的余弦值为
的余弦值为 …………13分
…………13分
又
 面ABB1A1,所以CC1//平面ABB1A1, …………2分
面ABB1A1,所以CC1//平面ABB1A1, …………2分ABCD是正方形,所以CD//AB,
又CD
 面ABB1A1,所以CD//平面ABB1A1, …………3分
面ABB1A1,所以CD//平面ABB1A1, …………3分所以平面CDD1C1//平面ABB1A1,
所以C1D//平面ABB1A1 …………4分
(II)解:ABCD是正方形,AD⊥CD
因为A1D⊥平面ABCD,
所以A1D⊥AD,A1D⊥CD,
如图,以D为原点建立空间直角坐标系D—xyz, …………5分

在
 中,由已知可得
中,由已知可得
所以
 ,
,
 …………6分
…………6分因为A1D⊥平面ABCD,
所以A1D⊥平面A1B1C1D1
A1D⊥B1D1。
又B1D1⊥A1C1,
所以B1D1⊥平面A1C1D, …………7分
所以平面A1C1D的一个法向量为n=(1,1,0
 ) …………8分
) …………8分设
 与n所成的角为
与n所成的角为 ,
,则
 …………9分
…………9分所以直线BD1与平面A1C1D所成角的正弦值为
 …………10分
…………10分(III)解:平面A1C1A的法向量为

则

所以

令
 可得
可得 …………12分
…………12分设二面角D—A1C1—A的大小为a,
则

所以二面角
 的余弦值为
的余弦值为 …………13分
…………13分
练习册系列答案
相关题目
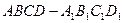 的底面为正方形,
的底面为正方形,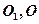 分别为上、下底面的中心,且
分别为上、下底面的中心,且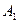 在底面
在底面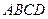 的射影是
的射影是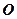 。
。 (Ⅰ)求证:平面
(Ⅰ)求证:平面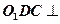 平面
平面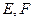 分别在棱上
分别在棱上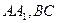 上,且
上,且 ,问点
,问点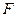 在何处时,
在何处时,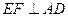 ;
;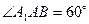 ,求二面角
,求二面角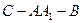 的大小(用反三角函数表示)。
的大小(用反三角函数表示)。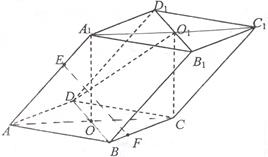
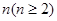 条直线,其中任意两条不平行,任意三条不共点。
条直线,其中任意两条不平行,任意三条不共点。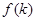 表示
表示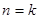 时平面被分成的区域数,则
时平面被分成的区域数,则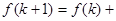 ( )
( )



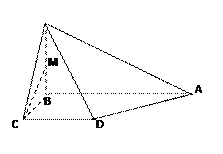
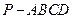 中,
中,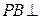 平面
平面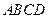 ,
, 底面
底面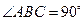 ,
,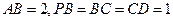 。
。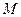 为
为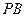 的中点,证明:直线
的中点,证明:直线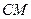 ∥平面
∥平面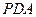 ;
;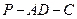 的余弦值。
的余弦值。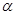 、
、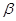 是两个不同的平面,m、n是平面
是两个不同的平面,m、n是平面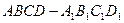 的棱长为
的棱长为 ,则点
,则点 到平面
到平面 的距离为
的距离为 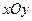 中,已知平面区域
中,已知平面区域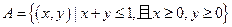 ,则平面区域
,则平面区域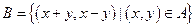 的面积为( )
的面积为( )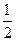
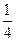
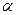 、
、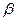 、
、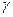 两两互相垂直,长为
两两互相垂直,长为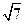 的线段AB在
的线段AB在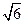 、a、b,则
、a、b,则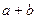 的最大值为 。
的最大值为 。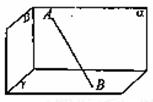
 ,
, ,
, 所成的角是 .
所成的角是 .