题目内容
已知数列{an}满足a1=1,且an=2an-1+2n(n≥2且n∈N+).
(1)求证:数列{
}为等差数列;
(2)设数列{an}的前n项和为Sn,求Sn.
(1)求证:数列{
| an |
| 2n |
(2)设数列{an}的前n项和为Sn,求Sn.
考点:数列的求和,等差关系的确定
专题:等差数列与等比数列
分析:(1)数列{an}满足a1=1,且an=2an-1+2n(n≥2且n∈N+).两边都除以2n可得
-
=1,即可证明;
(2)利用“错位相减法”与等比数列的前n项和公式即可得出.
| an |
| 2n |
| an-1 |
| 2n-1 |
(2)利用“错位相减法”与等比数列的前n项和公式即可得出.
解答:
(1)证明:∵数列{an}满足a1=1,且an=2an-1+2n(n≥2且n∈N+).
∴
-
=1,
∴数列{
}为等差数列,公差为1,首项
=
.
(2)解:由(1)可得:
=
+(n-1)×1=
.
∴an=(2n-1)×2n-1.
Sn=1+3×2+5×22+…+(2n-3)×2n-2+(2n-1)×2n-1,
2Sn=2+3×22+5×23+…+(2n-3)×2n-1+(2n-1)×2n,
∴-Sn=1+2×2+2×22+…+2×2n-1-(2n-1)×2n=
-1-(2n-1)×2n=(3-2n)×2n-3,
∴Sn=(2n-3)×2n+3.
∴
| an |
| 2n |
| an-1 |
| 2n-1 |
∴数列{
| an |
| 2n |
| a1 |
| 21 |
| 1 |
| 2 |
(2)解:由(1)可得:
| an |
| 2n |
| 1 |
| 2 |
| 2n-1 |
| 2 |
∴an=(2n-1)×2n-1.
Sn=1+3×2+5×22+…+(2n-3)×2n-2+(2n-1)×2n-1,
2Sn=2+3×22+5×23+…+(2n-3)×2n-1+(2n-1)×2n,
∴-Sn=1+2×2+2×22+…+2×2n-1-(2n-1)×2n=
| 2×(2n-1) |
| 2-1 |
∴Sn=(2n-3)×2n+3.
点评:本题考查了等差数列的通项公式、“错位相减法”与等比数列的前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
已知平面区域D1={(x,y)|
},D2={(x,y)|kx-y+2<0,k>0},在区域D1内随机选取一点M,且点M恰好在区域D2上的概率为p,若0<p≤
,则k的取值范围为( )
|
| 1 |
| 4 |
| A、k≥2 | ||
| B、0<k≤1 | ||
| C、k≥1 | ||
D、0<k≤
|
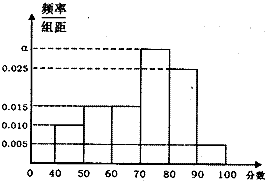 某校从参加高三年级期中考试的学生中随机抽出60名学生,将其中考试的政治成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如下部分频率分布直方图.
某校从参加高三年级期中考试的学生中随机抽出60名学生,将其中考试的政治成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如下部分频率分布直方图.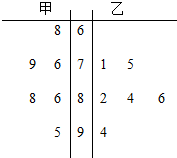 在科普知识竞赛前的培训活动中,将甲、乙两名学生的6次培训成绩(百分制)制成如图所示的茎叶图:
在科普知识竞赛前的培训活动中,将甲、乙两名学生的6次培训成绩(百分制)制成如图所示的茎叶图: