题目内容
9．已知扇形的半径为1cm，圆心角为2rad，则该扇形的面积为1cm2．分析 直接求出扇形的弧长，然后求出扇形的面积即可．
解答 解：扇形的圆心角为2，半径为1，扇形的弧长为：2，
所以扇形的面积为：$\frac{1}{2}×1×2$=1．
故答案为：1．
点评 本题是基础题，考查扇形的面积的求法，弧长、半径、圆心角的关系，考查计算能力．
练习册系列答案
名校课堂系列答案
相关题目
19．已知复数z满足z=$\frac{4+3i}{1+2i}$，则z=（ ）
| A． | 2+i | B． | 2-i | C． | 1+2i | D． | 1-2i |
20．在正方体ABCD-A1B1C1D1中，（$\overrightarrow{{A}_{1}{D}_{1}}$-$\overrightarrow{{A}_{1}A}$）-$\overrightarrow{AB}$=（ ）
| A． | $\overrightarrow{{D}_{1}A}$ | B． | $\overrightarrow{A{D}_{1}}$ | C． | $\overrightarrow{B{D}_{1}}$ | D． | $\overrightarrow{{D}_{1}B}$ |
17．等差数列{an}中，a1=2016，前n项和为Sn，若$\frac{{S}_{12}}{12}$-$\frac{{S}_{10}}{10}$=-2，则S2016=（ ）
| A． | 2014 | B． | 2015 | C． | 2016 | D． | 2017 |
18．已知函数f（x）是定义在R上的奇函数，f（2）=0，当x＞0时，有$\frac{xf'（x）-f（x）}{x^2}＞0$成立，则不等式x2f（x）＞0的解集是（ ）
| A． | （-2，0）∪（2，+∞） | B． | （-2，0）∪（0，2） | C． | （2，+∞） | D． | （-∞，-2）∪（2，+∞） |
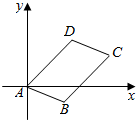如图，已知平行四边形ABCD的三个顶点的坐标分别为A（0，0），B（2，-1），C（4，2）．