题目内容
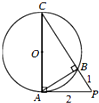如图PA是圆O的切线，切点为A，PA=2，AC是圆O的直径，PC与圆O交于点B，PB=1，则圆O的半径R=（ ）| A、2 | ||
| B、3 | ||
C、
| ||
D、
|
考点：弦切角
专题：立体几何
分析：由圆的切割线定理，得到PA2=PB•PC，求出BC，由直径所对的角为直角，运用勾股定理即可求出圆的半径．
解答：
解：由于PA是圆O的切线，切点为A，PA=2，PB=1，PBC为圆的割线，
由切割线定理得，PA2=PB•PC，
即PC=4，BC=3，
在直角三角形ABP中，AB=
=
，
在直角三角形ABC中，AC=
=2
，
∴圆O的半径R为
．
故选D．
由切割线定理得，PA2=PB•PC，
即PC=4，BC=3，
在直角三角形ABP中，AB=
| 4-1 |
| 3 |
在直角三角形ABC中，AC=
| 3+9 |
| 3 |
∴圆O的半径R为
| 3 |
故选D．
点评：本题主要考查圆的切割线定理及运用，以及直径所对的角为直角，勾股定理的运用，是一道基础题．
练习册系列答案
相关题目
已知△ABC中，
⊥
，|
-
|=2，点M是线段BC（含端点）上的一点，且
•（
+
）=1，则|
|的取值范围是（ ）
| AB |
| AC |
| AB |
| AC |
| AM |
| AB |
| AC |
| AM |
A、（
| ||
B、[
| ||
| C、（1，2] | ||
D、（1，
|
方程log3x=x-4的一个实根所在的区间是（ ）
| A、（2，3） |
| B、（3，4） |
| C、（5，6） |
| D、（6，7） |
⊙O1：x2+y2=1与⊙O2：（x-3）2+（y+4）2=9，则⊙O1与⊙O2的位置关系为（ ）
| A、相交 | B、外切 | C、内切 | D、外离 |
已知一个算法，其流程图如图所示，则输出结果是（ ）
| A、7 | B、10 | C、13 | D、16 |
已知直线l过点P（4，3），圆C：x2+y2=25，则直线l与圆的位置关系是（ ）
| A、相交 | B、相切 |
| C、相交或相切 | D、相离 |
在四棱锥P-ABCD中，∠ABC=∠ACD=90°，∠BAC=∠CAD=60°，PA⊥面ABCD，E为PD之中点，PA=2AB=2