题目内容
已知直线l过点P(4,3),圆C:x2+y2=25,则直线l与圆的位置关系是( )
| A、相交 | B、相切 |
| C、相交或相切 | D、相离 |
考点:直线与圆的位置关系
专题:直线与圆
分析:根据题意判断P在圆C上,确定出直线l与圆的位置关系即可.
解答:
解:∵P(4,3),圆C(0,0),r=5,
∴
=5,即|PC|=r,
∴点P在圆C上,
∵直线l过点P,
∴直线l与圆的位置关系是相交或相切.
故选:C.
∴
| (4-0)2+(3-0)2 |
∴点P在圆C上,
∵直线l过点P,
∴直线l与圆的位置关系是相交或相切.
故选:C.
点评:此题考查了直线与圆的位置关系,直线与圆的位置关系由d与r的大小来判断,当d=r时,直线与圆相切;当d<r时,直线与圆相交;当d>r时,直线与圆相离.

练习册系列答案
相关题目
在如图以O为中心的正六边形上随机投一粒黄豆,则这粒黄豆落到阴影部分的概率为( )


A、
| ||
B、
| ||
C、
| ||
D、
|
若AD为△ABC的中线,现有质地均匀的粒子散落在△ABC内,则粒子在△ABD内的概率等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=sin(
-x)(x∈R),下面结论正确的是( )
| π |
| 2 |
A、函数f(x)的最小正周期为
| ||
B、函数f(x)在区间[0,
| ||
| C、函数f(x)是奇函数 | ||
| D、函数f(x)的图象关于直线x=0对称 |
从装有3个红球、2个白球的口袋里随机取出一个球,得到红球的概率是( )
A、
| ||
B、
| ||
C、
| ||
| D、1 |
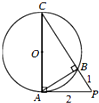 如图PA是圆O的切线,切点为A,PA=2,AC是圆O的直径,PC与圆O交于点B,PB=1,则圆O的半径R=( )
如图PA是圆O的切线,切点为A,PA=2,AC是圆O的直径,PC与圆O交于点B,PB=1,则圆O的半径R=( )