题目内容
求过两条直线x-2y+4=0和x+y-2=0的交点P，且满足下列条件的直线方程．
（1）过点Q（2，-1）；
（2）与直线3x-4y+5=0垂直．
（1）过点Q（2，-1）；
（2）与直线3x-4y+5=0垂直．
考点：待定系数法求直线方程
专题：直线与圆
分析：（1）联立方程组求得两条直线的交点坐标，可得它的斜率，再用点斜式求得直线PQ的方程．
（2）利用两条直线垂直的性质求得所求直线的斜率，再用点斜式求得所求直线的方程．
（2）利用两条直线垂直的性质求得所求直线的斜率，再用点斜式求得所求直线的方程．
解答：
解：（1）由
，解得
，∴P（0，2）．
∵kPQ=
=-
，∴直线PQ：y-2=-
x，即3x+2y-4=0．
（2）∵直线3x-4y+5=0的斜率k=
，
∴所求直线的斜率k′=-
，
∴所求直线为y-2=-
x，即4x+3y-6=0．
|
|
∵kPQ=
| 2+1 |
| 0-2 |
| 3 |
| 2 |
| 3 |
| 2 |
（2）∵直线3x-4y+5=0的斜率k=
| 3 |
| 4 |
∴所求直线的斜率k′=-
| 4 |
| 3 |
∴所求直线为y-2=-
| 4 |
| 3 |
点评：本题主要考查用点斜式求直线的方程，两条直线垂直的性质，属于基础题．
练习册系列答案
相关题目
下列命题中正确的是（ ）
| A、20.3＜1 | ||||
| B、?m，n∈R+，lg（m+n）=lgm•lgn | ||||
C、4 -
| ||||
D、若3
|
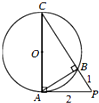如图PA是圆O的切线，切点为A，PA=2，AC是圆O的直径，PC与圆O交于点B，PB=1，则圆O的半径R=（ ）从装有3个红球、2个白球的口袋里随机取出一个球，得到红球的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
| D、1 |
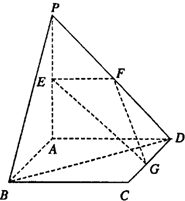如图，平面PAD⊥平面ABCD，ABCD为正方形，∠PAD=90°，且PA=AD=2，E、F、G分别是线段PA、PD、CD的中点．