题目内容
15.已知过抛物线x2=4y焦点F的直线交抛物线于A、B两点(点A在第一象限),若$\overrightarrow{AF}=3\overrightarrow{FB}$,则直线的方程为( )| A. | $\sqrt{3}x-y-\sqrt{3}=0$ | B. | $x-\sqrt{3}y+\sqrt{3}=0$ | C. | $x-\sqrt{3}y-1=0$ | D. | $\sqrt{3}x-y+1=0$ |
分析 根据直线方程可知直线恒过定点F(0,1),过A、B分别作BQ⊥l于Q,AP⊥l于P,BC⊥AP,垂足为C,由|AF|=3|FB|,则|AP|=3|BQ|,进而求得直线的斜率.
解答 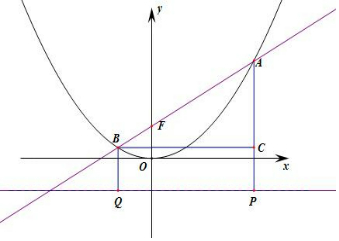 解:设抛物线C:x2=4y的准线为l:y=-1,焦点F(0,1)
解:设抛物线C:x2=4y的准线为l:y=-1,焦点F(0,1)
设直线AB:y=kx+1(k>0)
过A、B分别作AP⊥l于P,BQ⊥l于Q,BC⊥AP,垂足为C,
由|AF|=3|FB|=3m,则|AP|=3|BQ|=3m,∴|AC|=2m,|AB|=4m,|BC|=2$\sqrt{3}$m
∴k=$\frac{\sqrt{3}}{3}$,
则直线AB的方程:y=$\frac{\sqrt{3}}{3}$x+1,整理得:x-$\sqrt{3}$y+$\sqrt{3}$=0,
故选:B.
点评 本题主要考查了抛物线的简单性质,考查了对抛物线的基础知识的灵活运用,考查了数形结合的思想,属于中档题.

练习册系列答案
相关题目
5.设函数f(x)=Asin(ωx+φ)(A>0,ω>0),若f($\frac{π}{2}$)=f($\frac{2π}{3}$)=-f($\frac{π}{6}$),且f(x)在区间[$\frac{π}{6}$,$\frac{π}{2}$]上单调,则f(x)的最小正周期是( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | π |
10.已知函数f(x)=Asin(ωx+φ),x∈R(其中$A>0,ω>0,0<Φ<\frac{π}{2}$)的图象与x轴的交点中,相邻的两个交点之间的距离为$\frac{π}{2}$,且图象上的一个最低点为$M(\frac{2π}{3},-2)$,则f(x)的解析式为( )
| A. | $f(x)=2sin(2x+\frac{π}{6})$ | B. | $f(x)=2cos(2x+\frac{π}{6})$ | C. | $f(x)=sin(2x+\frac{π}{3})$ | D. | $f(x)=cos(2x+\frac{π}{3})$ |
20.已知函数f(x)=ax2+bx+c,且a>b>c,a+b+c=0,集合A={m|f(m)<0},则( )
| A. | 任意m∈A,都有f(m+3)>0 | B. | 任意m∈A,都有f(m+3)<0 | ||
| C. | 存在m∈A,都有f(m+3)=0 | D. | 存在m∈A,都有f(m+3)<0 |
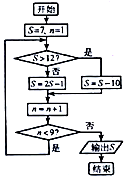 阅读如图的程序框图,运行相应的程序,则输出的S值为3.
阅读如图的程序框图,运行相应的程序,则输出的S值为3.