题目内容
9．
公元263年左右，我国古代数学家刘徽用圆内接正多边形的面积去逼近圆的面积求圆周率π，他从圆内接正六边形算起，令边数一倍一倍地增加，即12，24，48，…，192，…，逐个算出正六边形，正十二边形，正二十四边形，…，正一百九十二边形，…的面积，这些数值逐步地逼近圆面积，刘徽算到了正一百九十二边形，这时候π的近似值是3.141024，刘徽称这个方法为“割圆术”，并且把“割圆术”的特点概括为“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣”．刘徽这种想法的可贵之处在于用已知的、可求的来逼近未知的、要求的，用有限来逼近无穷，这种思想及其重要，对后世产生了巨大影响，如图是利用刘徽的“割圆术”思想设计的一个程序框图，若运行改程序（参考数据：$\sqrt{3}$≈1.732，sin15°≈0.2588，sin7.5°≈0.1305），则输出n的值为（ ）| A． | 48 | B． | 36 | C． | 30 | D． | 24 |
分析 列出循环过程中S与n的数值，满足判断框的条件即可结束循环．
解答 解：模拟执行程序，可得：
n=6，S=3sin60°=$\frac{3\sqrt{3}}{2}$，
不满足条件S≥3.10，n=12，S=6×sin30°=3，
不满足条件S≥3.10，n=24，S=12×sin15°=12×0.2588=3.1056，
满足条件S≥3.10，退出循环，输出n的值为24．
故选：D．
点评 本题考查循环框图的应用，考查了计算能力，注意判断框的条件的应用，属于基础题．
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
名师点睛字词句段篇系列答案
相关题目
20．执行如图所示的程序框图，如果输入N=30，则输出S=（ ）
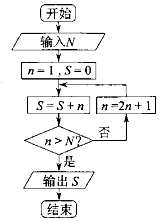
| A． | 26 | B． | 57 | C． | 225 | D． | 256 |
4．已知集合S={1，2}，设S的真子集有m个，则m=（ ）
| A． | 4 | B． | 3 | C． | 2 | D． | 1 |
1．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的离心率为$\frac{{\sqrt{2}}}{2}$，双曲线 x2-y2=1的渐近线与椭圆C有四个交点，以这四个交点为顶点的四边形的面积为8，则椭圆C的方程为（ ）
| A． | $\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{2}$=1 | B． | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{6}$=1 | C． | $\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1 | D． | $\frac{{x}^{2}}{20}$+$\frac{{y}^{2}}{5}$=1 |
18．为了响应厦门市政府“低碳生活，绿色出行”的号召，思明区委文明办率先全市发起“少开一天车，呵护厦门蓝”绿色出行活动，“从今天开始，从我做起，力争每周至少一天不开车，上下班或公务活动带头选择步行、骑车或乘坐公交车，鼓励拼车…”铿锵有力的话语，传递了低碳生活、绿色出行的理念．某机构随机调查了本市500名成年市民某月的骑车次数，统计如下：
联合国世界卫生组织于2013年确定新的年龄分段：44岁及以下为青年人，45岁至59岁为中年人，60岁及以上为老年人．记本市一个年满18岁的青年人月骑车的平均次数为μ．以样本估计总体．
（Ⅰ）估计μ的值；
（Ⅱ）在本市老年人或中年人中随机访问3位，其中月骑车次数超过μ的人数记为ξ，求ξ的分布列与数学期望．
 | [0，10） | [10，20） | [20，30） | [30，40） | [40，50） | [50，60] |
| 18岁至30岁 | 6 | 14 | 20 | 32 | 40 | 48 |
| 31岁至44岁 | 4 | 6 | 20 | 28 | 40 | 42 |
| 45岁至59岁 | 22 | 18 | 33 | 37 | 19 | 11 |
| 60岁及以上 | 15 | 13 | 10 | 12 | 5 | 5 |
（Ⅰ）估计μ的值；
（Ⅱ）在本市老年人或中年人中随机访问3位，其中月骑车次数超过μ的人数记为ξ，求ξ的分布列与数学期望．